Die komplexen Zahlen befinden sich auf einer Ebene und deshalb ist es aufwändiger mit ihnen zu rechnen. Bei Grenzwertberechnungen muss man in zwei Richtungen, der x-Achse und der y-Achse vorgehen, die hier einen neuen Namen haben. Für die Darstellung von komplexen Zahlen benutze ich auch die Vektorschreibweise. Sie ist schön übersichtlich. Man muss sich immer klar machen, dass der Vektor eigentlich eine andere Schreibweise für die Summe seiner Komponenten ist. Achtet darauf. Dann werdet ihr die Berechnungen gut nachvollziehen können.
Das Phänomen, dass das Quadrat einer imaginären Zahl i die reelle Zahl -1 ergibt, taucht immer wieder auf, so auch bei der Grenzwertberechnung der imaginären Funktion. Das Minuszeichen hat dann große Relevanz bei dem Ergebnis.
Ich gebrauche nur soweit Variablen, wie sie unbedingt notwendig sind, ansonsten lasse ich sie weg. Das macht die Darstellung übersichtlicher und leichter verständlich.
Für zwei winzige Differenzialgleichungen muss man ganz schön viel rechnen. Augen auf und durch!












Bürgerliche Darstellung
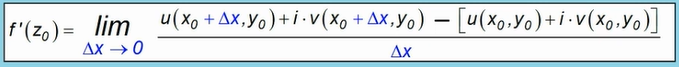
Auch die blaue Farbe macht diese Darstellung nicht klarer.
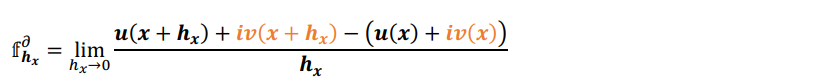
Die säxische Notation kommt mit weniger Informationen aus.