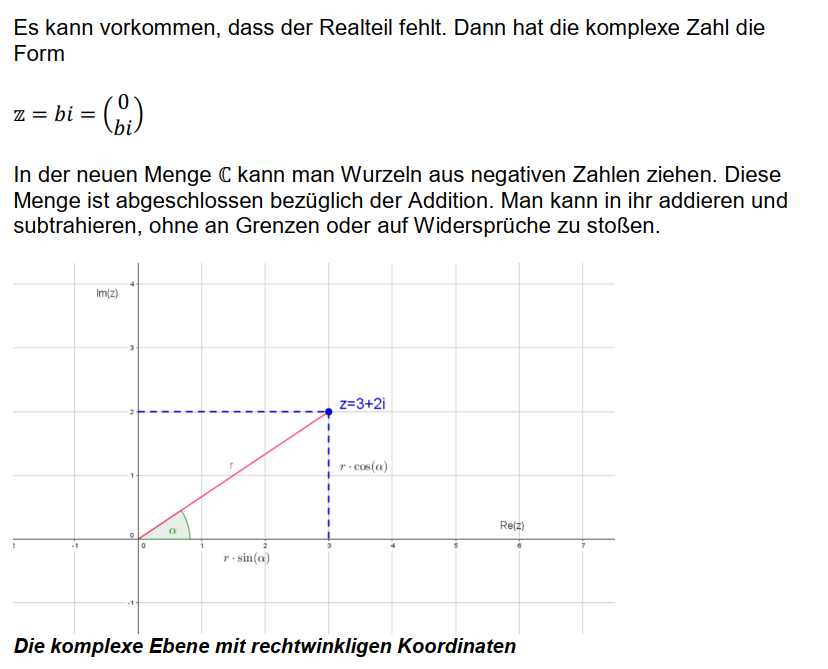
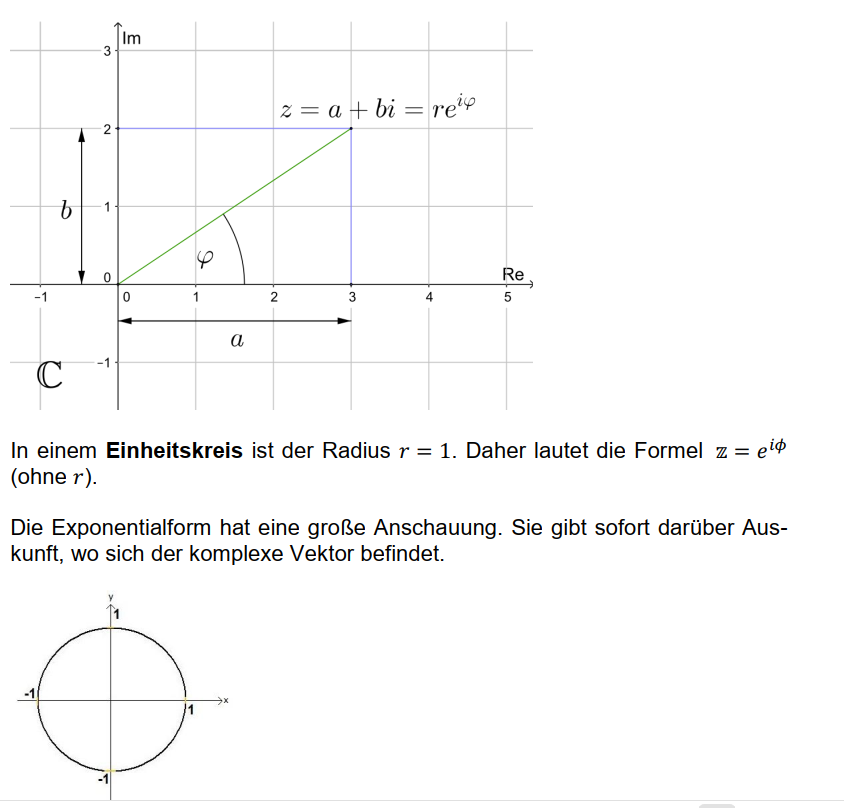
Die komplexen Zahlen bilden die Krönung der Zahlen. Endlich kann man mit allen Rechenoperationen umgehen, auch die Wurzel aus negativen Zahlen ziehen. Die komplexen Zahlen werden in der Ebene dargestellt und ihre Position über rechtwinklige oder polare Koordinaten bestimmt.
Den Einsatz des babylonischen Dreiecksatzes werde ich euch demonstrieren. Er ist bekannt als Satz des Pythagoras, der ihn aber nicht entwickelt hatte. Die Ehre gebe ich den alten Babyloniern zurück.
Warum man den Phasenfaktor e hoch iz mit der Summe von Cosinus und i-Sinus gleichsetzen kann, zeige ich am Schluss.