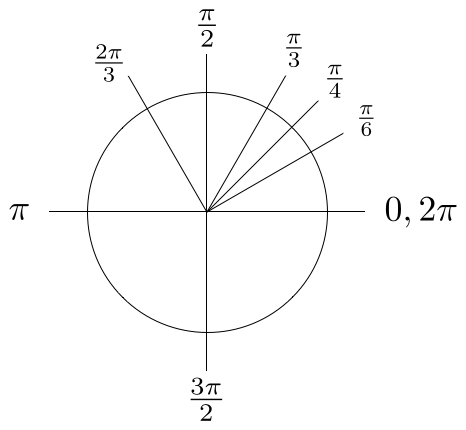
Der Einheitskreis spielt in der höheren Mathematik eine große Rolle. Er wird für die Vektorrechnung und komplexen Zahlen gebraucht und ist nicht mehr wegzudenken bei der Differenzialgeometrie, dem Themengebiet der Differenziale und der geometrischen Darstellung. Ich habe eine Neuerung bei der Bezeichnung des Kreisumfangs eingeführt, die der amerikanische Physiker Michael Hartl im Jahr 2010 vorgestellt hatte. Die Kreiskonstante heißt nun „tau“ und ersetzt das bislang benutzte „pi“. Die neue Bezeichnung hat vielfache Vorteile. Seine Länge beträgt ungefähr 6.2832 LE (Längeneinheiten).
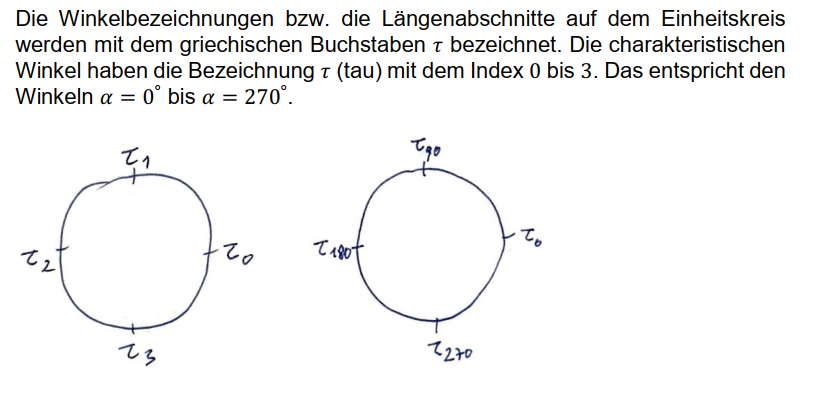
Mein bescheidener Beitrag ist die Indexsetzung beim „tau“. Ich habe das „tau“ je nach seiner Position am Einheitskreis von 0 bis 3 durchnummeriert. Die Winkel können ebenfalls angegeben werden.
Ich finde es schöner, zu sagen „tau 1“ statt „pi Halbe“. Gemeint ist der Winkel von 90 Grad beim Cosinus oder Sinus. Außerdem ist „tau 1“ ein Viertel des Einheitkreises. Man kann sich das wie bei der Uhr vorstellen.


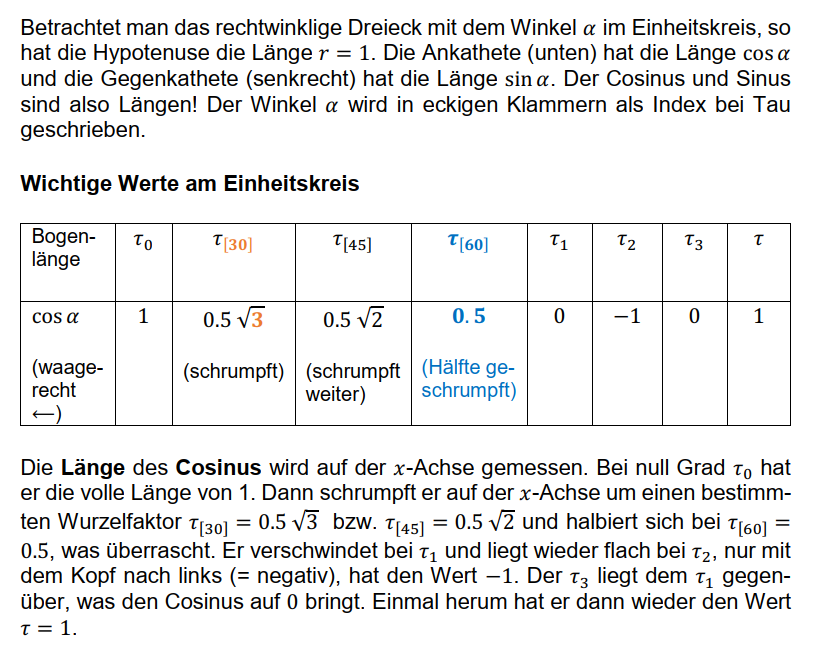
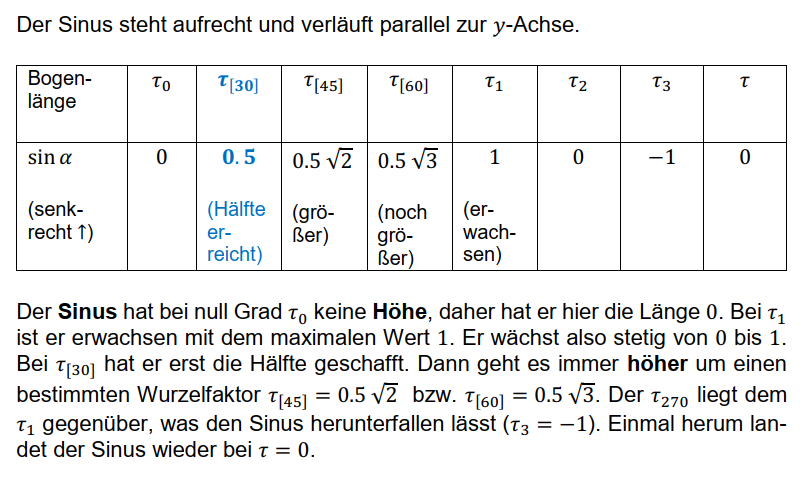
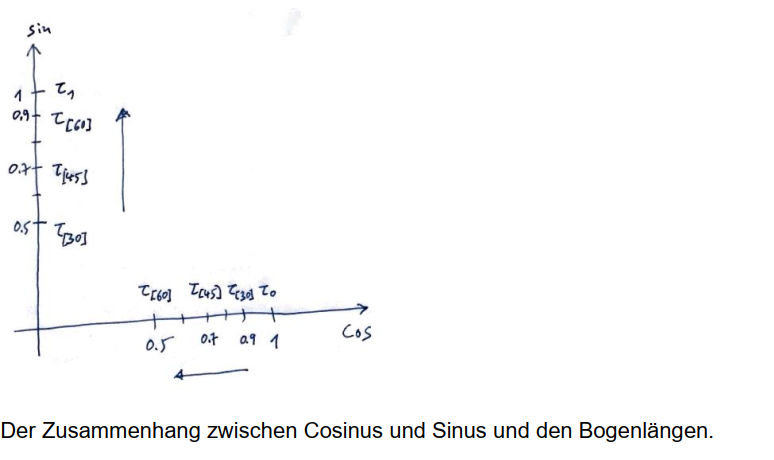
Hier seht ihr, dass der Cosinus bei größerem Winkel schrumpft und nach links zum Koordinatenursprung spaziert. Der Sinus hingegen reckt sich und wächst bis zum Maximalwert von 1. Lernt das auswendig. Es ist wirklich wichtig.
Das pi ist nun Vergangenheit!