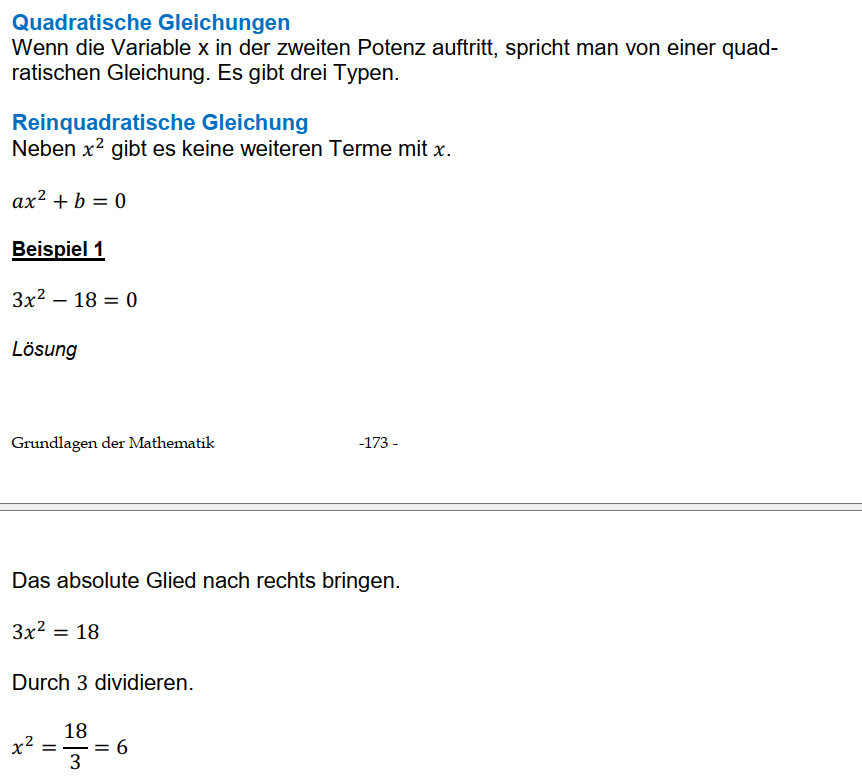
Was quadratische Gleichungen sind und wie man sie berechnen kann, stelle ich euch hier vor. Oft kommt man mit der quadratischen Ergänzung schneller voran als mit der p-q-Formel. Dazu habe ich ein Schema entwickelt, die Schnelllösung.
Die p-q-Formel ist aus der Schulzeit bekannt. Sie dient zur Lösung von quadratischen Gleichungen, In diesem Beitrag zeige ich euch, dass die Terme in einer quadratischen Gleichung nicht zwingend x enthalten müssen. Ich stelle euch eine Aufgabe vor, in der y angegeben ist. Das ist ungewohnt, sollte aber nicht davon abhalten, die Variablen p und q zu identifizieren und sie nach einer bestimmten Umwandlung in die säxische p-q-Formel einzusetzen.
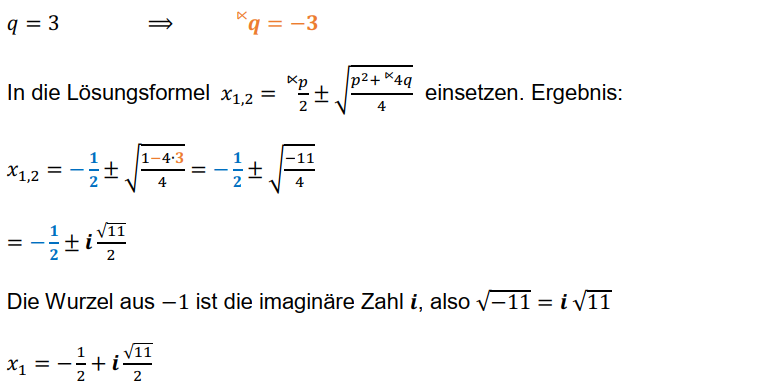
Außerdem löse ich eine quadratische Gleichung, deren Lösung eine komplexe Zahl ist. Das ist kein Hexenwerk. Ihr könnt dazu auch die p-q-Formel benutzen.
Die säxische Notation ist mehr intuitiv gestaltet.