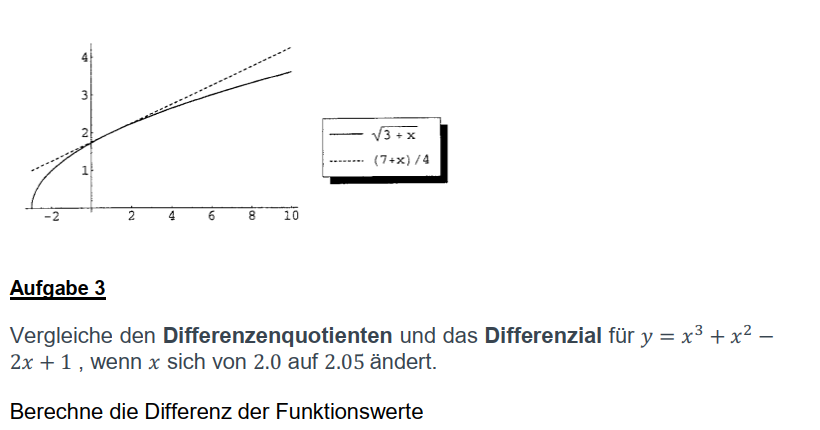
Die lineare Näherung von Funktionen ist ein nützliches Instrument. Dazu benutzt man die Näherungsgleichung, die so ähnlich wie eine lineare Funktion aussieht. Statt der Steigungsvariablen m wird der Differenzialoperator genommen. Das x der linearen Funktion ist bei der linearen Näherung eine Differenz aus dem x und dem Start-x.
Bei der Aufgabe 1 berechnet ihr den Differenzialoperator nicht über eine Ableitung, sondern aus den gemessenen Temperaturen zu verschiedenen Zeiten.