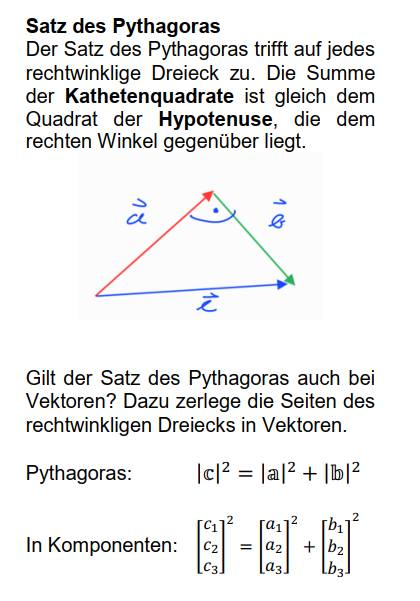
So langsam habe ich mich in die Vektorrechnung eingearbeitet. Das geht also auch im hohen Alter. Ich habe den Beweis ausformuliert, dass der Satz des Pythagoras auch bei Vektoren gilt. Man braucht nur die bekannte Formel mit dem a-Quadrat plus b-Quadrat gleich c-Quadrat und setzt beim Quadrat der Hypotenuse die Summe der beiden anderen Vektoren ein. Eine kleine algebraische Umformung und das Wissen, dass das Skalarprodukt von orthogonalen Vektoren null ist, führt zum gewünschten Ergebnis.
Der Satz des Pythagoras wird gebraucht, um die Länge von Vektoren zu berechnen. Er ist also ganz praktisch.
Meine Darstellung auf den Fotos kann doch jeder Abiturient verstehen. Ich erkläre jeden Rechenschritt und gebe kurze Hinweise. Das werdet ihr an der bürgerlichen Universität und auch in den bürgerlichen Lehrbüchern so nicht finden. Besonders hilfreich erachte ich meine neue Notation von Vektoren. Als Kontrastprogramm hat ich das letzte Foto beigefügt. Wie findet ihr diese Darstellung?
Die Hörsäle leeren sich immer mehr, je umfangreicher und abstrakter der Stoff in der Mathematik und Physik wird. Das muss doch nicht sein. Die jungen Leute sind hoch motiviert, haben Optimismus und Leistungswillen. Jedoch werden die meisten in den genannten Fächern scheitern. Ich sehe die Ursache in der mangelhaften Didaktik der Professoren und Dozenten und in der benutzten Symbolik, die häufig verwirrt. Wenn ich an die eckigen Klammern bei der Vektorrechnung denke, bekomme ich einen Anfall.
Vorgestern hatte ich einen Dozenten bei dem Verkettungssymbol mit dem Kringel gefragt, wer denn das erfunden hätte, worauf er verdutzt guckte und sagte „ich nicht“. Dieses Symbol muss man wie einen arabischen Text von rechts nach links lesen, haha. Das ist Verwirrung pur!
Ich glaube nicht, dass die bürgerlichen Universitäten hier Änderungen schaffen würden oder überhaupt Reformen in Gang setzen würden. Sie sind so fest gefahren wie die bürgerliche Gesellschaft auch.
Mein Mathematikbuch kommt voran und darüber freue ich mich.