Wie überhaupt das mathematische Denken entstand, wie die Menschen zu verschiedenen Ansichten kommen, kann uns nur ein Blick in die menschliche Entstehungsgeschichte geben. Neuere Funde in Afrika zeigen, dass der Australopithecus, was „südlicher Affe“ bedeutet, schon in der Lage war, selbstständig Waffen anzufertigen. Die Kriege haben also schon eine lange Tradition. Dazu nahm er den Unterkiefer mit den scharfen Zähnen bzw. den Vorderlauf einer bestimmten Antilopenart und legte sich damit an den Wasserlöchern, wo viele Tiere zusammenkommen müssen, auf die Lauer (wie geschickt!). Hatte er ein unvorsichtiges Tier erspäht, dann erschlug er es gemeinsam mit den anderen menschlichen Jägern. Dieser aufrecht gehende Australopithecus war aus einem Erbsprung (Mutation) entstanden, so dass er Fleisch verdauen konnte. Sein vegetarischer Vetter, genannt der robuste Südaffe (Australopithecus robustus) wegen seines starken Gebisses, konnte beim besten Willen kein Fleisch vertragen und wurde von seinen Vettern gerne verspeist.

Australopithecus Sediba (Quelle: profberger)
Erbsprünge waren es wiederum, die dem südlichen Raubaffen zudem menschlichen Gebiss verhalfen, wie es noch heute jeder Mensch trägt. Wahrscheinlich fiel ihm das Fell wegen bestimmter Genkopplungen aus z.B. größeres Wachstum des Gehirns bedingt die Umformung der Hände und des Haarwuchs und umgekehrt. Dieser Raubaffe, dessen Gehirn nicht größer als das eines heutigen Schimpansen war, wechselte in der Steppe seine Verhaltensweisen, weil er nicht anders konnte. Es gab keinen Weg mehr zurück auf die Bäume, woher er gekommen war (siehe unsere Greifhand), denn der Baumbestand nahm in gewaltigen Ausmaßen für Millionen Jahre lang ab.
Wo also hin?
Der Affe kletterte vom Baum und wurde Mensch. Als der Südaffe Fleisch verdauen konnte, jagte er sowohl Tier als auch sich, was an entsprechenden Funden erkennbar ist (Loch im Schädel mittels eines Antilopenvorderbeines). Sein Gehirn wuchs, weil durch die Jagdweise neue Verhaltensweisen erlernt und gespeichert werden sowie an die nachfolgenden Generationen weitergegeben (Tradition) werden mussten. Hierbei überlebten nur die Geschicktesten und Intelligentesten, die die Waffen (damals Überlebenswerkzeuge) verbessern konnten und auch vor den bösen Nachbarn auf der Hut waren. Die Menschheitsentwicklung lässt auf eine immer kompliziertere geistige Entwicklung bis hin zur modernen Wissenschaft schließen.
Erste Sprachansätze waren notwendig, wenn die gemeinsame Jagd erfolgreich sein sollte. Auch hier setzte sich eine Auslese zum Intelligenteren durch. Die heutigen Sprachen sind schon sehr hoch entwickelt und nicht vergleichbar mit den Ursprachen, die sicherlich schon Verben wie essen, hungern, jagen, schlafen und viele Nomen enthielten. Mit den affenartigen Stöhn- und Kreischlauten hätten die frühen menschlichen Jäger nichts anfangen können. Damit hätte niemand einen Faustkeil schaffen können und ihn sinngerecht einsetzen können.
Mit der Sprachentwicklung ging auch eine Vervollkommnung der Hand und der Werkzeugentwicklung einher. Der frei bewegliche Daumen ist die Grundvoraussetzung für das spätere Wirtschaften, sei es Viehzucht Landwirtschaft oder Industrie. Ohne die Sprache gäbe es keine Kultur, keine Schrift und keine Religion, auch keine Mathematik.
Nur Menschen denken über das Jenseits nach und haben allerlei Rezepte dafür geschaffen, um dahin zu gelangen. Oft haben sie das Jenseits so sehr betont, dass sie das Diesseits vernachlässigten. In der Mathematik kommt es jedenfalls nicht auf das Glauben an eine Heilslehre an. Was einmal bewiesen wurde, wird ewig bestehen bleiben. Da gibt es keine Sektenbildung, einen Zerfall oder Untergang wie bei den Religionen.
Die mathematische Sprache hat eine lange Geschichte. Sie beginnt in der Steinzeit. Die Menschen, die zählen konnten, waren die Cro-Magnon-Menschen. Deren Überreste hat man in Frankreich entdeckt. So sah dieser Mensch aus. Es ist die plastische Nachbildung einer Cro-Magnon-Frau. Ohne Schminke würde sie heute sicherlich nicht als Covergirl auf eine der bunten Illustrierten abgedruckt. Doch hatte sie schon das gleiche Gesicht wie die Damen von heute.

Cro-Magnon-Frau (Quelle: Ökologix)
Schon vor 30.000 Jahren machten die Menschen Mathematik, aber nicht mit Papier und Bleistift, sondern mit Knochen. Die kerbten sie ein. Man hat Knochen mit regelmäßigen Einkerbungen gefunden. Jeweils fünf Striche wurden zusammengefasst zu einer Gruppe. Das war schon Mathematik. Heute macht man das immer noch.

Ishango-Knochen (Quelle: Ben2)
Die frühen Menschen konnten schon gut zeichnen. In Höhlen hinterließen sie großartige Tiermalereien. Diese Höhlenmalereien stammen aus der Höhle von Lascaux im Tal der Vézère, das nahe von Montignac in Frankreich liegt. Sie wurden etwa 17.000 bis 15.000 Jahre vor unserer Zeitrechnung erstellt. Zu sehen sind gemalte Wildrinder, Pferde und Hirsche. Auch in Afrika gab es rechnende Menschen. Dort hat man Knochen mit Kerben gefunden. Damit hatte man offensichtlich schon gezählt.
Die Zahlzeichen wurden erst kann spät erfunden. Das war, als die Menschen sesshaft wurden und viel Zeit hatten. Sie brauchten die Zahlzeichen, um nachzählen zu können, wie viele Rinder, Schafe, Hühner und andere Haustiere sie hatten. Sie brauchten die Zahlen auch, um ihr Getreide zu wiegen, um Vorräte anzulegen, um einen Kalender anzufertigen. Für die Bauern ist die Zeit ganz wichtig. Sie müssen genau wissen, wann sie das Getreide aussäen können und wann sie es abmähen können. Dazu brauchten sie die Mathematik.
Es gab sehr unterschiedliche Symbole für Zahlen. Die Chinesen benutzten andere Symbole als die Babylonier oder Ägypter. Die braucht ihr nicht zu lernen. Es ist aber interessant zu wissen, wie sie aussahen. Die Menschen waren sehr erfinderisch. In unterschiedlichen Regionen der Erde erfanden sie recht verschiedene Zahlzeichen. Die römischen Zahlen werden noch heute benutzt. Die hast du bestimmt schon mal gesehen. Man schreibt damit Nummern.
In der Religion spielen Zahlen auch eine Rolle. Es gibt z. B. Gebetsschnüre bei den Buddhisten, Christen und Muslimen. Der Betende betet bei jeder Perle einen bestimmten Spruch. In Europa ist der Rosenkranz bekannt. Er wird in der katholischen Marienandacht benutzt. Damit der Beter richtig betet, nimmt er den Rosenkranz als Zählhilfe. So kann er sich nicht vertun. Man braucht zum Beten genau wie in der Mathematik viel Ausdauer. Wer viel übt, hat später auch viel Erfolg. Dran bleiben ist das A und O der Mathematik. Aus den Strichlisten und Kerbhölzern entwickelten sich die heutigen Zahlen. Die heißen arabische Ziffern, weil die Araber sie nach Europa gebracht hatten. Sie sehen unseren heutigen Zahlen recht ähnlich. Ohne Zahlen kommt man in der Mathematik nicht aus. Aber auch Buchstaben sind sehr wichtig in der Mathematik. Sie sind oft leicht verständliche Abkürzungen von Wörtern. Die kann man schnell lernen. Bestimmte Theoreme („mathematische Sätze“) zu verstehen dauert manchmal ziemlich lange.
„Als etwa um 300 v. Chr. der größte Geometriker Griechenlands, Euklid, in Alexandrien von seinem König Ptolemaeus Philadelphus nach einer ‚bequemen‘ Unterrichtsmethode der Mathematik gefragt wurde, erwiderte er kühn: ‚Zur Mathematik führt kein Königsweg.’” [Col42, Vorwort, Seite 10]
Bevor ich auf die Sprache und Symbolik der Mathematik eingehe, stelle ich die einfache Frage: „Was leistet die Mathematik?“
Die Antwort darauf ist ebenfalls einfach.
Die Mathematik vermittelt eine Denkweise, die überall gebraucht wird, ob beim Einkaufen, bei der Arbeit oder beim Sterben, auch hier ist Mathematik nötig und sei es, wie viel Zuckerkuchen später beim Leichenschmaus bestellt werden soll und wie teuer die Bestattung sein wird.
Die Mathematik wird man einfach nicht los. Sie hängt an jedem wie eine Klette, höchst unbeliebt, doch irgendwie notwendig.
Vor allem Schüler hassen sie aus tiefstem Herzen – von einigen Ausnahmen abgesehen, die von der Allgemeinheit bedauert werden.
Unsere Vorfahren vor tausenden vor Jahren konnten nur bis drei zählen. Darüber hinaus begnügten sie sich mit der Angabe viele. In dem deutschen Wort „vier“ steckt noch dieser unbestimmte Begriff „viele“. Da lacht man heute drüber, doch damals reichte das völlig aus. Erst mit einer höheren gesellschaftlichen Entwicklung waren die Menschen gezwungen, ihren Wortschatz zu erweitern, auch die Zahlbegriffe. Manche Völker nahmen ihre Finger als Maßstab und zählten bis 10. Andere meinten, da könnte man noch zwei Zahlen drauflegen und rechneten mit der 12 als Grundlage ihres Zahlensystems. Warum nicht mehr nehmen, dachten sich andere Völker und schauten auf ihre Zehen, die dann eine neue Grundlage ihres Zahlensystems bildeten. Die heutigen Franzosen, man glaubt es kaum, sagen zu 80 quatre vingt, also 4 mal 20! Ein mathematisches Erbe aus alter Zeit. Das hat sie aber nicht dran gehindert, bedeutende Mathematiker hervorzubringen.
Das indische Wort sunya (das Leere) wurde zu arabisch sifr, dann latinisiert cifra. Die Franzosen machten daraus zero (= Null), was sich auch im Englischen so wieder findet. Das deutsche Wort Ziffer bezieht sich allerdings nicht nur auf die Null allein, sondern auch alle anderen 10 Zahlzeichen. Aus diesen Zahlzeichen (= Ziffern) wird unser Zehnerzahlensystem zusammengesetzt. Die Zahlen von 0 bis 10 sind mit den Ziffern identisch, aber ab 11 aufwärts beginnt das Reich der Zahlen, ein buntes Gemisch aus beliebigen Ziffern. Wer hier Zahlen mit Ziffern verwechselt, hat nicht verstanden, dass die Ziffern nur eine Teilmenge der Zahlen sind.
In unserer Gesellschaft ging es wieder abwärts auf die 2 als Grundlage der Zahlbildung, eine Dekadenzentwicklung. Weil man damit überhaupt nicht als Mensch umgehen kann, hat der Homo sapiens Maschinen erfunden, die Taschenrechner und Computer, die das mit einer Schnelligkeit machen, die einen ins Staunen versetzen. Trotzdem sind die PCs strohdumm und ärgern immer wieder schlaue Programmierer, weil sie partout nicht das machen, was sie eigentlich machen sollten.
Schon in der Schule werden Taschenrechner eingesetzt, die den Schülern die Mathematik nahe bringen und sie bei der Lösung von Aufgaben unterstützen sollen. Dadurch lernen sie zwar, auf die richtigen Tasten zu drücken, was aber Mathematik bedeutet, bleibt ihnen fremd. Mit diesem Buch soll sich das ändern, ein großer Anspruch – oder bleibt es bloß bei einem Versuch? Der Leser wird es heraus finden.
„Was dem Gedächtnis nicht von selbst (inwendig!) sich einverleibt, das ist nicht verstanden, nicht verdaut. Darum wiederhole! Du mußt alles Fremde in Eigenes umwandeln, so macht’s jeder lebende Organismus.”
[Rod42a, 1. Band, Seite 6]
Die Mathematik hat eine eigene Sprache. Die besteht aus lauter Abkürzungen und Buchstaben mit kleinen Zahlen wie zum Beispiel hier:
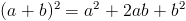
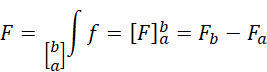
Die Kürzel haben alle eine bestimmte Bedeutung. Das könnt ihr alles lernen. Mathematik ist ja mehr als eins und eins zusammenzählen wie in der Grundschule. Das dauert aber alles seine Zeit. Wenn ihr alt und grau seid, werdet ihr das alles können. Es gibt noch andere berühmte Griechen. Sie waren ganz tolle Mathematiker.
Interesse und Ausdauer sind in der Mathematik wichtig. Ohne Ausdauer kann man die Mathematik nicht lernen. Man darf nie aufgeben. Wer sagt, ich kann das nicht, und nichts tut, bleibt wirklich dumm.
Die Mathematik ist wie ein Spiel. Je mehr ihr mit ihr spielt, desto schöner wird dieses Spiel sein und desto mehr werdet ihr begreifen, was die Mathematik alles an Schönem bietet. Spielt also mal mit den Zahlen und Buchstaben. Probiert aus, was ihr mit ihnen alles machen könnt. In der Mathematik darf man viel spielen. Sie macht richtig Spaß und bringt viel Freude.
Ein Mathematikbuch kann man nicht wie einen Roman von oben nach unten durchlesen. Man versteht es immer besser, wenn man es mehrfach durchliest. Wenn ihr etwas vergessen habt, ist das nicht schlimm. Einfach nachlesen. Ohne Üben geht es jedoch nicht. Aber das macht auch Spaß, besonders wenn man danach alles kann.
„Aber was du ganz er- und verarbeitet hast, das bleibt dir dann ganz von selbst wörtlich haften und ist dir in Fleisch und Blut übergegangen. Das sitzt.” [Rod42a, 1. Band, Seite 6]
Quellen
Australopithecus Sediba: profberger, siehe http://de.wikipedia.org/wiki/Australopithecus (geprüft am 05.07.2012)
Cro-Magnon-Frau: Ökologix, siehe: http://de.wikipedia.org/wiki/Cro-Magnon-Mensch (geprüft am 05.07.2012)
Ishango-Knochen: Ben2, siehe: http://de.wikipedia.org/wiki/Ishango-Knochen (geprüft am 05.07.2012)
[Col42] Egmont Colerus: Vom Einmaleins zum Integral. Mathematik für Jedermann. Karl H. Bischoff Verlag, Berlin, Wien, Leipzig, 1942
[Rod42a] Rode, Hanns R. (1942): Das technische Rechnen 1. Ein Handbuch zum Selbststudium: Arithmetik und Algebra. 11. Auflage. 3 Bände. Berlin: Verlag der Deutschen Arbeitsfront