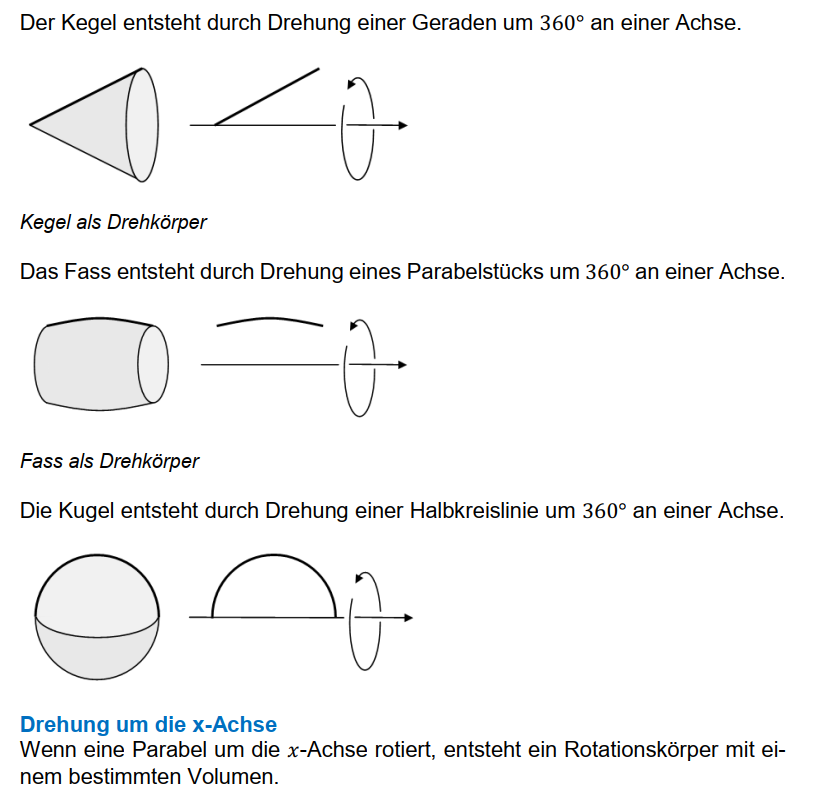
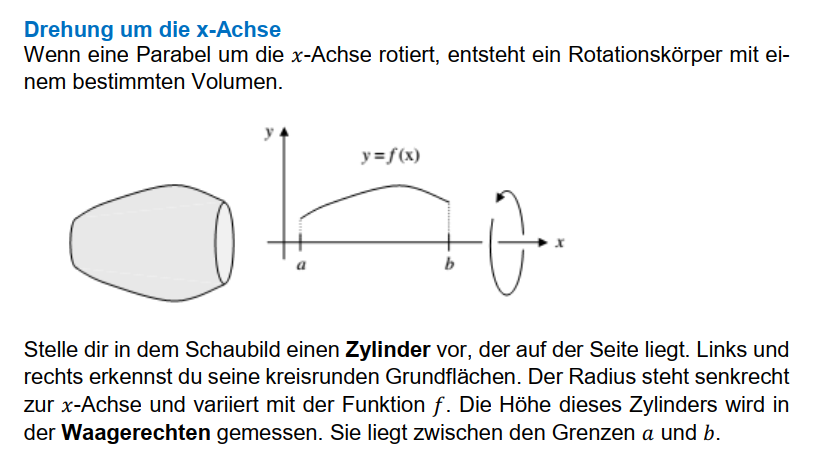
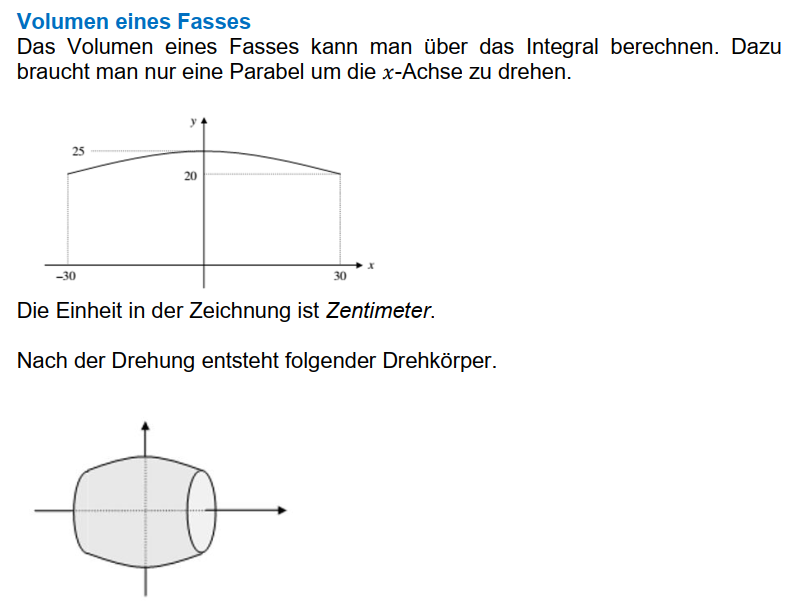
Die Integralrechnung bietet die Möglichkeit, das Volumen von unregelmäßigen Körpern zu berechnen, sofern es eine Funktionsgleichung dafür gibt. Die Formel dazu beruht auf dem Volumen eines Zylinders. Durch geschickte Einbettung des Integrals in diese Formel kann man schnell das Volumen eines Rotationskörpers errechnen.
Es ist wichtig, die Notation von Integralen zu verstehen. Die Integrationsgrenzen entsprechen der Höhe des Zylinders. Der Radius wird beschrieben durch die gegebene Funktion der Aufgabe. Wenn man sich einen umgefallenen Zylinder vorstellt, kann man diese Angaben bei den entsprechenden Variablen in der Formel für das Zylindervolumen wieder finden.