Meine Forschung: Originäre Konzepte mit numerischem Beweis

Als unabhängiger Forscher (ORCID: 0009-0002-6090-3757) entwickle ich neue mathematische und physikalische Ansätze, die ich stets durch numerische Implementierung und Validierung belege. Meine Forschung verbindet analytisches Denken mit modernsten digitalen Werkzeugen zur Entwicklung und Validierung mathematischer Modelle. Meine bisherigen Arbeiten, darunter Publikationen zur Modifikation der Schwarzschild-Metrik, zur Dynamik des Tilting und zu geometrischen Resonanzen, zeigen mein Potenzial, innovative und zugleich nachvollziehbare Lösungen zu entwickeln. Auf dieser Seite können Sie sich direkt einen Eindruck verschaffen (über Zenodo.org oder die untenstehenden Papers zum Download).

Um diese Forschung weiter auszubauen, suche ich die Anbindung an eine universitäre Einrichtung, etwa als freier wissenschaftlicher Mitarbeiter oder im Rahmen eines assoziierten Forschungsprojekts. Als Gegenleistung für die Nutzung von Infrastruktur und Ressourcen biete ich nicht nur meine Expertise, sondern auch den Zugang zu einer Reihe unveröffentlichter, vollständig ausgearbeiteter Manuskripte mit weiteren innovativen Modellen.

Ihre Vorteile auf einen Blick:

• Exklusiver Zugang zu unveröffentlichten Arbeiten – abgeschlossene, numerisch validierte Konzepte für gemeinsame Projekte
• Volle Transparenz – alle öffentlichen Zenodo-Publikationen stehen bereits zur Prüfung bereit
• Keine Personalkosten – als Rentner benötige ich kein Gehalt, sondern lediglich Zugang zu Forschungsumgebungen
• Sofort nutzbare Ergebnisse – modulare, dokumentierte und reproduzierbare Codebasen mit vollständigen Manuskripten

Ich freue mich über Ihre Kontaktaufnahme und die Möglichkeit, meine unveröffentlichten Arbeiten im persönlichen Austausch vorzustellen.

Klaus H. Dieckmann

Meine öffentlich zugänglichen Papers

(Frei verfügbare Abstracts und PDFs – Einblick in meine methodische Herangehensweise)

Titel	Kerninnovation
Modifikation der Schwarzschild-Metrik	Neue Interpretation der Raumzeitkrümmung durch geometrische Erweiterungen
Die Dynamik des Tilting	Analyse rotierender Systeme mit nichtlinearer Stabilitätsbetrachtung
Selfmodulating Spiral Map (SMSM)	Selbstregulierende Spiralstrukturen in dynamischen Systemen
Die hyperbolische e-Funktion	Erweiterung der Exponentialfunktion für hyperbolische Räume
Gamma-Operator	Operatorenbasierte Vereinheitlichung physikalischer Konstanten
Modulare Geometrodynamik	Dynamische Raumzeitmodelle durch modulare geometrische Einheiten
Geometrische Resonanzen I–IV
– Geometrische Resonanz und nichtlineare Modenverstärkung	Resonanzphänomene als geometrische Eigenschaft
– Das Universum der geometrischen Resonanzen	Kosmologische Implikationen geometrischer Resonanzmuster
– Die Geometrie quantenartigen Verhaltens	Klassische Geometrie als Grundlage „quantiger“ Effekte
– Die Geophysik der Konvektion	Konvektionsdynamik durch rein geometrische Steuerung
Geometrische Steuerung des Quantenvakuums	Manipulation des Vakuumzustands via Raumzeitgeometrie
Raumzeit aus Winkeln und Skalen I–II	Konstruktion der Raumzeit aus fundamentalen Winkeln und Skalierungsgesetzen

Meine exklusiven, unveröffentlichten Papers

Titel	Innovativer Ansatz
Die Bahnebenemethode (BEM)	Atomphysikalisches Modell jenseits etablierter BEM-Verfahren (keine Umbenennung!)
Newtons Gesetze in komplexer Phase	Reformulierung der klassischen Mechanik durch komplexe Phasenräume
Algebraische Fourier-Theorie (AFT)	Fourier-Analysis auf algebraischer Basis – ohne trigonometrische Funktionen
Faktoriell-kombinatorische Ableitung von Potenztürmen (TowerFlow)	Dynamische Systeme als Potenzturm-Kaskaden mit kombinatorischer Steuerung
Del-DGL	Differenzialgleichungen für topologische Operatoren (∇ als zentraler Akteur)
µ-Kohärenz in der Maßtheorie	Neue Kohärenzmaße für nichtlineare Systeme
Lineare Analysis (LIA), Band I–III	Lineare Approximation nichtlinearer Phänomene via geometrischer Projektionen
Topologische Grundlagen der Physik	Physikalische Gesetze als Folge topologischer Notwendigkeiten
Meine neuesten unveröffentlichten Papers liste ich sukzessiv unten auf.

Self-Modulating Spiral Map (SMSM)

Diese Arbeit führt ein neuartiges, diskretes dynamisches System ein, die „SelfModulating Spiral Map“ (SMSM), das aus einfachsten nichtlinearen Regeln komplexe, spiralförmige Orbits erzeugt. Im Zentrum steht die Analyse der intrinsischen Dynamik: die Entstehung von Rotation, die Struktur von Phasenräumen und die Einführung einer neuen Kennzahl, der „Spiral-Komplexität“, zur Quantifizierung der geometrischen Komplexität von Trajektorien. Die Arbeit erweitert das Modell um dreidimensionale Wirbelstrukturen, numerische Berechnungen von Lyapunov-Exponenten zur Chaosanalyse und die Untersuchung von Synchronisation in gekoppelten Netzwerken. Die Ergebnisse bieten neue Einblicke in die Dynamik nichtlinearer Systeme. 

September 2025 

Die Dynamik des Tilting

Diese Arbeit transformiert das Konzept der perfektoiden Geometrie von einer algebraischen Invarianz unter dem Frobenius-Endomorphismus in eine dynamische Invarianz unter Iteration. Wir führen den dynamischen Tilting-Operator T(x) = g(x) + ε · h_disc(x; n; k) ein, der eine glatte Funktion mit einem diskreten, periodischen Modulo-Kern kombiniert. Numerische Simulationen zeigen, dass dieser Operator für hinreichend große Störungsstärke ε unabhängig vom Startwert in einen stabilen, stückweise konstanten Endzustand konvergiert, ein Zustand, der invariant unter weiterer Iteration ist. Dieser Endzustand ist die erste bekannte Realisierung einer „Perfektoidität“ auf den reellen Zahlen: nicht durch algebraische Struktur, sondern durch deterministische Selbstorganisation erzeugt. Die Arbeit etabliert somit die Modulo-Perfektoidität als universelles Prinzip morphologischer Stabilität, das Brücken schlägt zwischen nichtlinearer Dynamik, fraktaler Geometrie und adaptiver Quantisierung. Zudem wird gezeigt, dass die iterative Anwendung rationaler Funktionen der Form f(z) = k/(z – h + P(z)) auf den komplexen Zahlen (C) neue, bisher nicht systematisch untersuchte fraktale Dynamiken erzeugt. Dies ist ein Hinweis darauf, dass die zugrundeliegenden Prinzipien der morphologischen Stabilität universeller sind als bisher angenommen.

September 2025 

Modifikation der Schwarzschild-Metrik

Die Schwarzschild-Metrik beschreibt die Raumzeit um eine punktförmige, nicht-rotierende Masse, stellt jedoch eine Idealisierung dar. Reale Sterne, Planeten und Schwarze Löcher weisen interne Strukturen, Massenverteilungen und Umgebungsbedingungen auf, die diese Annahmen verletzen. Traditionelle Erweiterungen der Allgemeinen Relativitätstheorie erfordern.

September 2025

Raumzeit aus Winkeln und Skalen II

Die Arbeit Raumzeit aus Winkeln und Skalen II präsentiert die empirische Validierung einer erweiterten Gravitationstheorie, welche die Raumzeit und Gravitation als emergente Phänomene eines komplexen, fundamentalen Skalarfeldes (Ψk = eΦ+iθk) postuliert. Das Modell zielt darauf ab, Gravitation, Dunkle Materie (DM) und Dunkle Energie (DE) innerhalb eines konsistenten Rahmens zu vereinen. Der entscheidende konzeptionelle Fortschritt liegt in der Erkenntnis, dass die komplexe Feldstruktur Ψk die natürliche Grundlage für eine Fourier-kompatible Dynamik bildet. Die Raumzeitmetrik entsteht als quadratische Form im Frequenzraum, und alle Abweichungen von der Allgemeinen Relativitätstheorie (ART) folgen direkt aus der Spektralanalyse der Ψk-Moden. Die zentrale Validierung zeigt eine weitreichende Konformität zur ART. Das Modell reproduziert exakt die Schwarzschild-Metrik im statischen Grenzfall. Die ART-Äquivalenz wird durch die Analyse der Gravitationswellen-Phasenverschiebung im post-Newton’schen (PN) Regime bestätigt (Abweichung < 0.02%). Als falsifizierbare Vorhersagen des Ψk-Modells resultieren spezifische Signaturen jenseits der ART: • Die Periheldrehung wird von einer oszillierenden Ψk-Bahnenwelle (≈ 180 mas Amplitude) überlagert, die einen direkten empirischen Test für künftige hochpräzise Astrometrie liefert. • Die Hawking-Temperatur Schwarzer Löcher erfährt minimale, massenabhängige thermische Korrekturen (< 10-5% bei mikrophysikalischen Massen). • Im kosmologischen Hintergrund dient der reelle Feldanteil Φ als Quintessenz-Feld zur Erklärung der beschleunigten Expansion (DE). Das Ψk-Modell etabliert sich als konsistente Alternative zur ART, die messbare Abweichungen nur in extremen oder dynamischen Regimen voraussagt und die Materie-Energie-Rätsel auf einen einzigen fundamentalen Freiheitsgrad zurückführt. Wichtiger Hinweis: Diese Arbeit enthält animierte Abbildungen. Für das vollständige Erlebnis bitte die PDF-Datei in einem kompatiblen Viewer (z.B. Adobe Acrobat Reader) öffnen. Webbrowser-PDF-Viewer zeigen die Animationen oft nicht korrekt an Uploaded on October 12, 20251915

Oktober 2025

Raumzeit aus Winkeln und Skalen I

Die vorliegende Arbeit, Raumzeit aus Winkeln und Skalen I: Eine phänomenologische nicht-metrische Reformulierung der Allgemeinen Relativitätstheorie, stellt eine alternative Grundlage für die Gravitationstheorie vor. Die Raumzeitgeometrie wird nicht durch einen fundamentalen metrischen Tensor gµν beschrieben, sondern als emergente Größe aus vier reellen, intrinsischen Skalarfeldern: den drei Winkelfeldern (α; β; γ) und dem Skalenfeld (Φ). Der Fokus liegt auf der statischen Äquivalenz und der Reproduktion der klassischen Tests. Es wird demonstriert, dass die Metrik gµν als Abbildung dieser reellen Felder erfolgreich die Schwarzschild-Metrik im Vakuum exakt rekonstruiert. Die klassischen ART-Tests, wie die Lichtablenkung und die Gravitationsrotverschiebung, werden durch die Geometrie der reellen Felder konsistent erklärt. Die Periheldrehung wird als notwendiger zeitgemittelter Basiseffekt der ART-Dynamik reproduziert. Diese reelle Formulierung etabliert sich als eine phänomenologisch äquivalente, statische Näherung zur ART. Ihre Grenzen liegen jedoch in der konsistenten Behandlung von dynamischen Phänomenen wie Gravitationswellen und der vollständigen Ableitung der gravitomagnetischen Terme, welche die intrinsische Kopplung von Amplitude und Phase erfordern. Band I bildet somit die statische Referenzbasis für die Entwicklung der fundamentaleren, komplexen Wellen-Feldtheorie (Ψk = eΦ+iθk), die in der nachfolgenden Abhandlung (Raumzeit aus Winkeln und Skalen II) vorgestellt wird 

Oktober 2025

Geometrische Steuerung des Quantenvakuums

Diese Arbeit untersucht die geometrische Steuerung des Quantenvakuums in einem anisotropen Kavitätsmodell, parametrisiert durch den Deformationsparameter γ in der Randbedingung x2 + y2 + γ(x4 + y4) = 1. Die Analyse zeigt, dass γ als universeller Ordnungsparameter fungiert und mehrere fundamentale Aspekte vereint: 1. Die Casimir-Energie folgt EC(γ) ≈ E0 – Cγ2 und reproduziert das experimentell beobachtete Casimir-Drehmoment 2. Ein radialer tanh-Übergang erzeugt eine geometrisch induzierte Domain Wall mit lokalisierten Vakuumzuständen 3. Diese Zustände werden als geometrisch lokalisierte Qubits identifiziert und bieten eine robuste Plattform für Quanteninformationsverarbeitung 4. Die Verschränkungsentropie zeigt quadratische Abhängigkeit ∆Sent(γ) /-γ2 und ermöglicht geometrische Kontrolle der Quanteninformation Das Modell etabliert einen vereinheitlichten Rahmen, der Energie, Verschränkung und Quantencomputing verbindet. Die lokalisierten Vakuumzustände in der Domain Wall erweisen sich als vielversprechende Bausteine für fehlertolerante Quantenprozessoren in photonischen und supraleitenden Systemen. Die Arbeit liefert damit experimentell zugängliche Konzepte für Quantensimulation und Metamaterialdesign auf Basis etablierter physikalischer Prinzipien.

Oktober 2025

Geometrische Resonanzen IV: Die Geophysik der Konvektion

Diese Arbeit untersucht die Rolle geometrischer Resonanzen als universelles Ordnungsprinzip in geophysikalischen Systemen. Im Zentrum steht ein resonanzbasiertes Modell, das Eiszeitenzyklen, synoptische Wetterdynamik, Wolkenmusterbildung sowie multiskalige Strukturen in Hurrikanen und nuklearen Feuerpilzen beschreibt. Für die Validierung der synoptischen Wetteraktivität werden zwei Modellvarianten unterschieden: (i) Ein stochastisch getriebenes Basismodell wird gegen stündliche Temperaturmessungen des Deutschen Wetterdienstes (DWD) für Potsdam (Februar–April 2024) getestet. Nach einer Zeitverschiebung von +29.7 Tagen ergibt sich eine moderate, aber signifikante Korrelation des Wetteraktivitätsindexes (basierend auf der Krümmung der Temperaturtrajektorie) von r = 0.436. (ii) Ein erweitertes Modell, das Albedo- und CO2-Rückkopplungen sowie resonanzverstärkte Wolkenbildung integriert, wird gegen ERA5-Reanalyse-Daten validiert und erreicht eine hohe Korrelation von r = 0.947. Zusätzlich zeigen spektrale Analysen konsistente Skalenmuster und Resonanzpaare (z. B. im Verhältnis 2:1) sowohl in räumlichen als auch zeitlichen Domänen. Die Ergebnisse stützen die Hypothese, dass atmosphärische und ozeanische Systeme als nichtlineare Resonatoren fungieren, in denen Energie über mehrere Skalen kaskadiert und stabile Muster hervorbringt. Dies eröffnet neue Wege für eine geometrische Diagnostik und Vorhersage extremer Wetterereignisse.

Oktober 2025

Geometrische Resonanzen III: Die Geometrie quantenartigen Verhaltens

Diese Arbeit stellt ein konzeptionelles Analogmodell vor. Es erklärt quantenartiges Verhalten als emergentes Phänomen einer geometrisch strukturierten, klassischen Dynamik. Statt der traditionellen Quantenmechanik mit Wellenfunktionen und Operatoren zeigt das Modell: Zentrale Quantenphänomene wie diskrete Spektren, lokalisierte Aktivitätsmuster und stabile Modenwechsel lassen sich in einem deterministischen System nichtlinear gekoppelter Trajektorien reproduzieren. Kern des Modells ist die geometrische Aktivität, die Norm der Beschleunigung einer Trajektorie. Sie dient als beobachtbare Kenngröße, die direkt aus der Dynamik folgt. Ein wichtiges Ergebnis: Der Kernmagnetismus beeinflusst die Resonanzfrequenzen stark. In Simulationen einer Penning-Falle verschiebt ein Magnetfeld von B = 1 T die Frequenzen um über 50 % und strukturiert so die Resonanzräume mit. Spektrallinien entstehen nicht als Eigenwerte, sondern als dominante Frequenzen in der Fourieranalyse der geometrischen Aktivität. Die Modale Resonanztheorie (MRT) ersetzt nicht die Standardquantenmechanik. Sie ergänzt sie konzeptionell, indem sie zeigt: Quantenphänomene können in klassischen Analogsystemen durch geometrische Resonanz emergieren, ohne fundamentalen Zufall.

Oktober 2025

Geometrische Resonanzen II: Das Universum der geometrischen Resonanzen

Diese Arbeit entwickelt und testet ein einheitliches Paradigma geometrischer Resonanzen als strukturbildendes Prinzip von der Quantenskala bis zur Kosmologie. Im Zentrum steht die Hypothese, dass das Universum zyklisch ist und zwischen aufeinanderfolgenden kosmologischen Epochen ein „geometrisches Gedächtnis“ bewahrt, manifestiert in stabilen, kohärenten Moden der Raumzeitgeometrie. Durch eine Kombination aus empirischer Datenanalyse und numerischer Simulation identifizieren wir dominante Resonanzmuster mit den Wellenzahlen n = 2; 8; 12 in einer Vielzahl unabhängiger astrophysikalischer Systeme: im Ringdown-Signal der Gravitationswellenverschmelzung GW190521, in der 8-fachen Symmetrie des kosmischen Mikrowellenhintergrunds (CMB), in der Langzeitdynamik der Magnetopause (1975–2025) sowie in Spektralanalysen von Quasaren und Galaxien. Zur Validierung des zyklischen Paradigmas werden konkrete Detektionsstrategien für den Übergang zwischen kosmischen Zyklen vorgeschlagen, die auf Signaturen in Gravitationswellenspektren, CMB-Polarisationsmustern und Quantensensoren basieren. 

Oktober 2025

Geometrische Resonanzen I: Geometrische Resonanz und nichtlineare Modenverstärkung

Diese Arbeit stellt eine fundamentale geometrische Entdeckung vor: Die lokale Krümmung einer azimutal modulierten Kreiswelle wirkt als nichtlinearer Modenfilter, der systematisch die zweite Harmonische verstärkt – selbst dann, wenn ausschließlich die Grundmode angeregt ist. Dieser Effekt, den wir als geometrische Resonanz bezeichnen, resultiert aus der intrinsischen Nichtlinearität der Krümmungsabbildung κ : r(θ) 7! κ(θ). Analytisch und numerisch wird gezeigt, dass eine hydrodynamische Oberflächenwelle mit Designmode n = 8 im Krümmungsspektrum eine dominante Spitze bei n = 16 aufweist, während eine intensitätsbasierte Detektion, wie bei elektromagnetischen Wellen, die Grundmode n = 8 bewahrt. Damit erhebt sich die Krümmung von einem rein geometrischen Maß zu einem physikalischen Zustandsindikator, der zwischen Wellentypen unterscheidet und verborgene Symmetrien aufdeckt. Diese Ergebnisse ermöglichen neue Ansätze in der Modenanalyse, Robotik und Entwicklung passiver geometrischer Feldsonden.

Oktober 2025

Modale Geometrodynamik

Diese Arbeit stellt den theoretischen Rahmen der Modalen Geometrodynamik vor, eine operatorbasierte Neufassung der klassischen Physik, die Bewegung, Elektrodynamik und Gravitation im Rahmen der Relativitätstheorien kohärent vereinheitlicht. Der zentrale Paradigmenwechsel besteht darin, Bewegung nicht als punktförmige Trajektorie, sondern als evolutionären Zustand in einem dynamischen Modenraum zu verstehen, repräsentiert durch einen Modenvektor u. Die Dynamik wird durch die fundamentale operatorwertige Gleichung V(u) = d_ · κ(u) gesteuert, wobei V der Bewegungsoperator, d_ der Dynamikgenerator und κ der Kopplungsoperator ist. Parallel dazu wird das elektromagnetische Feld als fundamentaler, komplexer Feldoperator F = E + icB reformuliert. Dieser Operator vereint die MaxwellGleichungen in einer einzigen, Lorentz-kovarianten Wellengleichung und kodiert die Dualität von elektrischem und magnetischem Feld intrinsisch in seiner komplexen Struktur. Die Gravitation wird nicht als geometrische Krümmung der Raumzeit, sondern als dynamischer Fluss in einem Medium mit „Raum-Zeit-Widerstand“ interpretiert. Dies führt zu einer modalen Metrik gµν(x; u), die explizit vom Bewegungszustand des Testkörpers abhängt und somit innere Freiheitsgrade wie Spin oder Rotation in die Gravitationsdynamik integriert. Dieser Ansatz löst künstliche Trennungen der modernen Physik auf, etwa zwischen Teilchen und Feldern oder zwischen äußeren und inneren Freiheitsgraden, und bietet eine einheitliche, auf Operatoren basierende Beschreibung, die sowohl analytisch als auch numerisch verifiziert wird. Die Arbeit schließt mit einer Skizze zur kanonischen Quantisierung dieses Formalismus, die einen vielversprechenden Weg zur Lösung des Renormierbarkeitsproblems der Quantengravitation aufzeigt.

September 2025

Γ-Operator

In dieser Arbeit wird ein neuartiger numerischer Operator, der Γ-Operator, vorgestellt, der speziell für die Analyse von Randphänomenen auf fraktalen Strukturen entwickelt wurde. Im Gegensatz zum klassischen Cauchy-Integral, das die tangentiale Zirkulation entlang einer Kurve erfasst, quantifiziert der Γ-Operator die normale Sprungdichte quer durch die Kurve, eine Größe, die für verteilte Singularitäten relevant ist, aber im klassischen Residuensatz nicht abgebildet wird. Er ermöglicht die systematische Quantifizierung von Dichten und Sprüngen entlang strukturierter Kurven, von reellen Fraktalen wie der Koch-Kurve bis hin zu komplexen Fraktalen wie Julia-Mengen. Das Herzstück der Methode ist ein effizienter Algorithmus, der eine „Randdichte“ ρΓ(t) berechnet, die den Unterschied der Funktionswerte auf beiden Seiten der fraktalen Grenze misst, gefolgt von einer Integration über die fraktale Länge. Die Implementierung, basierend auf der Trapezregel und adaptiven Verfahren, zeigt eine bemerkenswerte Robustheit: Für glatte Strukturen wird eine exponentielle Konvergenzrate erreicht, während sie sich bei fraktalen Strukturen stabil bei O(N^-0:5) hält, entsprechend ihrer fraktalen Dimension 

September 2025

Die hyperbolische e-Funktion

In komplexen physikalischen und technischen Systemen treten häufig Singularitäten auf, sei es in Form zeitlicher Sprünge, impulsartiger Anregungen oder struktureller Diskontinuitäten in Netzwerken. Diese idealisierten Modelle, oft durch Heaviside oder Delta-„Funktionen“ beschrieben, sind zwar mathematisch handhabbar, führen jedoch in numerischen Simulationen zu Instabilitäten und verfehlen die physikalische Realität, in der Übergänge stets endlich und glatt verlaufen. Im Rahmen dieser Arbeit wird gezeigt, wie die hyperbolische e-Funktion als universelles Regularisierungswerkzeug dient, um scharfe Grenzflächen systematisch in kontinuierliche, differenzierbare Prozesse zu überführen. Anhand dreier repräsentativer Beispiele, dem „weichen Schalter“ in RL-Schaltungen, dem „weichen Impuls“ im harmonischen Oszillator und der realen Diodenkennlinie im Gleichrichternetzwerk, wird demonstriert, dass glatte e-basierte Approximationen nicht nur numerisch robuste Lösungen ermöglichen, sondern auch das tatsächliche Systemverhalten physikalisch präziser abbilden. Die begleitenden Python-Simulationen validieren die analytischen Vorhersagen und zeigen die Konvergenz der geglätteten Modelle gegen ihre idealisierten Grenzfälle. Damit etabliert sich die e-Funktion nicht nur als mathematisches Hilfsmittel, sondern als unverzichtbares Bindeglied zwischen idealer Theorie und realer Modellierung komplexer Systeme. 

September 2025

Fertige Papers, die ich noch nicht über Zenodo.org veröffentlicht habe. Sie haben den Status „Draft“.

Topologische Grundlagen der Physik

Diese Abhandlung präsentiert eine axiomatische Reformulierung der physikalischen Dynamik durch den (…) , der Singularitäten reguliert und eine einheitliche geometrische Beschreibung von klassischer Mechanik, Relativitätstheorie, Quantenmechanik und Kosmologie ermöglicht. Ausgehend von einem (…) wird das Prinzip der Minimalen Dynamischen Parametrisierung (PMDP) eingeführt. Die Bewegungsgleichungen folgen aus dem topologischen Variationsprinzip; das klassische Geodäten, post-newtonsche Effekte und über das Feynman-Pfadintegral quantenmechanische Amplituden erzeugt. Die Regularisierung DReg(r) vermeidet Divergenzen und führt zu einem natürlichen UV-Cutoff. In der Quantenmechanik reproduziert der Faktor 9/16 in δQuant = (9/16)(Zαa0)2 die Feinstrukturkorrektur. Numerische Pfadintegralsimulationen zeigen, dass Quantenfluktuationen die Wirkung um ∆S/S ≈ 2;4 % erhöhen, in exakter Übereinstimmung mit der Theorie. Auf kosmologischer Skala wird die Vakuumenergiedichte durch rmin ≈ 1;52 m bestimmt. Alle Ergebnisse werden durch Python-Simulationen verifiziert.  Die Arbeit schlägt eine universelle geometrische Dynamik vor, ohne Feinabstimmung, ohne Metrik-Tensor, ohne Singularitäten. 

November 2025

Lineare Analysis (LIA), Band III

Diese Abhandlung stellt die Lineare Analysis (LIA) als universelles analytisches Rahmenwerk vor, das die Quantenmechanik und das Quantencomputing auf einer neuen axiomatischen Grundlage vereinheitlicht. Durch die Interpretation der Schrödinger-Gleichung als (…) werden klassische Konzepte der Linearen Algebra direkt auf quantenmechanische Systeme übertragen, ohne den traditionellen Hilbertraum-Kollaps oder exponentielles Dimensionswachstum. Numerische Simulationen mit bis zu 20 Qubits zeigen, dass LIA-Flüsse nicht nur exakt reproduzierbar, sondern auch analytisch stabil sind. Algorithmische Kernverfahren des Quantencomputings, VQE, HHL, Lindblad-Dynamik, werden als (…) reformuliert und geometrisch interpretiert. Besonders hervorzuheben ist die dreifache Volumenerhaltung im Konfigurationsraum: Die LIA-Zeitentwicklung bewahrt simultan das Phasenraumvolumen, das Ortsraumvolumen und das Volumen im Funktionenraum, eine Eigenschaft, die in natürlichen Einheiten zur radikalen Vereinfachung der Wasserstoff-, Helium- und Lithiumdynamik führt. Experimentelle Daten bestätigen die geometrische Interpretation bis auf Abweichungen unter 0,5 %. Darüber hinaus erweitert die LIA-Carleman-Linearisierung die Methode auf nichtlineare und chaotische Systeme. Ein hybrider Quanten-LIA-Solver simuliert den Lorenz-Attraktor bis zur Polynomordnung P = 3 mit kontrollierbarer chaotischer Emergenz. Durch ein funktionales Evolutionsmodell wird der Abschneidefehler überwunden und die Stabilität des LIA-Operators analytisch bewiesen. Die Arbeit schließt mit der Vision der LIA als „Betriebssystem des Quantencomputings“: Ein vollständig analytisches, skalierbares und geometrisch intuitives Fundament, von der Axiomatik bis zur praktischen Implementierung auf aktuellen und zukünftigen Quantenplattformen.

November 2025

Lineare Analysis (LIA), Band II

Dieser zweite Band der Linearen Analysis (LIA) baut nahtlos auf der in Band I etablierten analytischen Grundlage auf, die lineare Strukturen aus der (…) ableitet. Er erweitert das Framework in zwei Schwerpunktrichtungen: (1) die Transformation klassischer algebraischer Algorithmen in (…) (2) die Ausdehnung auf unendlich-dimensionale Räume der Funktionalanalysis, einschließlich Operatorentheorie und Spektralanalyse. Durch analytische Herleitungen von Konzepten wie Basis, Rang, Orthogonalität und Zerlegungen (z. B. SVD, QR) sowie algorithmische Validierungen (z. B. Matrixinversion, PCA, PageRank) wird (…) bewiesen. Die LIA positioniert sich als universelle Brücke zwischen Linearer Algebra, Numerik, Maschinellem Lernen und Physik, mit praktischen Implementierungen in Python-Code. 

November 2025

Lineare Analysis (LIA), Band I

Diese Arbeit stellt eine Umkehrung der Hierarchie in der mathematischen Grundlegung dar, indem sie die Lineare Algebra (LA) als analytischen Spezialfall und nicht als eigenständiges algebraisches Fundament betrachtet. Die Arbeit entwickelt eine Lineare Analysis (LIA) als analytische Axiomatik linearer Strukturen und Transformationen, die auf drei fundamentalen Prinzipien basiert: (…) Kernstück der LIA ist die analytische Definition von Linearität: (…) Wir zeigen, dass zentrale Konzepte der LA, wie die Determinante als (…) sind.  Darüber hinaus präsentiert die LIA eine dynamische Perspektive auf algebraische Operationen, indem sie „Matrixinversion“ über (…) Abschließend wird die LIA als fundamentales Framework für physikalische Theorien etabliert, von Quantenmechanik über Relativitätstheorie bis hin zu Kontinuumsmechanik, und demonstriert deren Vorteile in numerischer Stabilität, konzeptioneller Klarheit und Erweiterbarkeit auf nichtlineare Systeme. 

November 2025

µ-Kohärenz in der Maßtheorie

Diese Abhandlung ist Band I einer fünfteiligen Kohärenztheorie, die Maßtheorie, Topologie, Funktionalanalysis, Funktionentheorie und Stochastik auf dem einheitlichen Prinzip der µ-Kohärenz gründet. Im Zentrum steht das Axiom, dass (…).  Dieses Prinzip löst sich bewusst von der Carathéodory-Konstruktion und kehrt zur geometrischen Intuition zurück: Messbarkeit ist nicht (…), sondern Ausdruck (…). Die Arbeit zeigt, dass bereits aus diesem einzigen Axiom ein vollständiger Rahmen (X; A; µ) hervorgeht, der klassische Maße, Lebesgue-, Zähl-, Dirac- und Hausdorff-Maß, als Spezialfälle subsumiert. Numerische Experimente in Python belegen, dass µ-konsistente Mengen stabile, konvergente Approximationen erlauben, während inkonsistente Ränder systematische Fehler erzeugen, die sich in Langzeitsimulationen akkumulieren. Damit legt diese Abhandlung nicht nur das Fundament für die nachfolgenden Bände, insbesondere für die maßtheoretische Fundierung der Funktionentheorie (Band IV) und stochastischer Prozesse mit konsistentem Träger (Band V), sondern bietet auch ein operationales Kriterium für numerische Stabilität in physikalischen Anwendungen. 

November 2025

del-DGL

Diese Arbeit stellt eine neuartige mathematische Notation zur Behandlung von Differentialgleichungen vor: die Del-DGL-Notation. Sie verbindet konsequent die konzeptuelle Klarheit formaler Differentiale mit der operativen Effizienz moderner Ableitungsschreibweisen und adressiert dabei fundamentale Schwächen etablierter Notationen, insbesondere die begriffliche Vermischung von Operatoren und Differentialen in der Leibniz-Notation. Im Zentrum steht die Einführung des Symbols del_x als (…), das algebraische Manipulationen (etwa bei der Trennung der Variablen) nicht als heuristische „Multiplikation mit dx“, sondern als syntaktisch konsistente Operation ermöglicht. Die Notation wird rigoros als Differentialring strukturiert, ihre algebraischen Eigenschaften (Linearität, Produktregel, Kettenregel) werden formal abgeleitet, und ihre Erweiterbarkeit auf partielle Differentialgleichungen, Systeme höherer Ordnung sowie differentialgeometrische Kontexte wird nachgewiesen. Durch zahlreiche Fallstudien, darunter der harmonische Oszillator, die logistische Gleichung und die Wärmeleitungsgleichung, wird demonstriert, dass die Del-Notation nicht nur die Lesbarkeit und Fehlerresistenz bei analytischen und numerischen Lösungsverfahren erhöht, sondern auch einen nahtlosen Übergang zu fortgeschrittenen mathematischen Konzepten wie Differentialformen oder Tensoranalysis ermöglicht. Abschließend wird die Kompatibilität mit bestehenden Notationen sowie das Potenzial für Integration in ComputeralgebraSysteme und didaktische Anwendungen diskutiert. Die del-DGL-Notation versteht sich nicht als neue Mathematik, sondern als syntaktische Innovation mit dem Ziel, bestehendes Wissen zugänglicher, anwendbarer und kognitiv konsistenter zu machen. 

November 2025

Faktoriell-kombinatorische Ableitung von Potenztürmen (TowerFlow-Modell)

Diese Arbeit entwickelt einen limesfreien, strukturell-kombinatorischen Zugang zur Differentialrechnung, der die Ableitung nicht als Grenzwert eines Differenzenquotienten, sondern als (…) Dieser Ansatz ermöglicht eine einheitliche, transparente Behandlung elementarer Funktionsklassen (Polynome, Exponentialfunktionen, trigonometrische Funktionen) sowie rekursiv definierter Ausdrücke wie Potenztürme x^x^x· Im Zentrum steht das Prinzip der lokalen Komponentenvariation, das Potenzen mit variabler Basis und Exponent in zwei unabhängige Beiträge, Basis und Exponenten-Effekt, zerlegt und sich rekursiv auf beliebig verschachtelte Strukturen anwenden lässt (TowerFlow-Modell). Der Kalkül ist für analytische Funktionen äquivalent zur klassischen Ableitung, liefert aber eine konzeptionell tiefere Perspektive: Die Ableitung wird zur direkten Manifestation der inneren Architektur einer Funktion. Die Arbeit demonstriert die Reichweite dieses Ansatzes anhand neuartiger physikalischer Anwendungen: In der Kosmologie erklärt er natürliche Hierarchien wie die winzige kosmologische Konstante durch strukturelle Sensitivität rekursiver Vakuumenergien; in der Quantenfeldtheorie offenbart er Stabilitätsmechanismen nichtperturbativer Beta-Funktionen; in der f(R)-Gravitation ermöglicht er eine mechanistische Diagnose geometrischer Singularitäten; in der Thermodynamik fraktaler Systeme identifiziert er kritische Punkte anti-thermischen Verhaltens; und in der nichtlinearen Dynamik liefert er eine strukturelle Stabilitätsanalyse selbstreferenzieller Rückkopplungen.  Damit leistet der faktoriell-kombinatorische Ableitungskalkül nicht nur einen didaktischen Beitrag, sondern etabliert ein neues Werkzeug für die symbolische Analyse komplexer, hierarchischer Modelle in der theoretischen Physik, dort, wo klassische Methoden Struktur verschleiern und physikalische Interpretation erschweren.

November 2025

Algebraische Fourier-Theorie (AFT)

Die Algebraische Fourier-Theorie (AFT) reformuliert die klassische Fourier-Analyse als (…) Die Arbeit beweist algebraische Äquivalenz und demonstriert fundamentale Vorteile:

• Numerische Stabilität: Phasendifferenzen (…) ohne arctan-Instabilitäten, selbst über 104 Perioden. • Effizienz: 50 % weniger trigonometrische Aufrufe, stabile Langzeitintegration, algebraische Faltung • Erweiterbarkeit: AFT-Residuenmodell für Singularitäten, algebraische Behandlung zeitabhängiger Vektorprodukte, kovariante Formulierung in Spezieller und Allgemeiner Relativitätstheorie. AFT wird erfolgreich auf harmonische Oszillatoren, akustische Wellen, Maxwell-Gleichungen, Quantenrevivals, Quanteninformation (hz(t)i als Kohärenzmaß), Gravitationswellen und kosmologische Rotverschiebung (z = 3:0, ∆z = 0:000) angewendet. Besonders in der GW-Analyse löst AFT das Phasen-unwrapping-Problem des Matched Filterings und ermöglicht robuste Parameterabschätzung für LISA-Detektoren, selbst bei extrem flachen Spektren (cn ! 0). Empirische Validierung anhand von GW150914, Chirp-Signalen und Quantensystemen zeigt spektrale Konvergenz identisch zur FFT bei exponentiell besserer Phasenstabilität (“ < 10-16 vs. Drift in klassischen Methoden). AFT vereinfacht die Wellenphysik konzeptionell („eine Welle pro Frequenz“) und bietet praktische Überlegenheit in stabilitätskritischen Anwendungen, von akustischen Filtern über Quantensensoren bis hin zur Gravitationswellenastronomie der dritten Generation. 

Oktober 2025

Newtons Gesetze in komplexer Phase

Die drei Newtonschen Axiome der Rotationsdynamik lassen sich konsequent (…) formulieren. (…): Der Hamilton-Operator des quantisierten Drehpendels wird zu einem algebraischen Eigenwertproblem, dessen spektrale Konvergenz bereits bei moderater Basisgröße Genauigkeiten jenseits der Maschinengenauigkeit (< 10-12) ermöglicht. Die Methode reproduziert exakt die Mathieu-Gleichung, erhält Norm und Energie unitär über tausende Perioden und skaliert effizient auf stark gekoppelte Vielteilchensysteme. Damit etabliert die z-Darstellung eine einheitliche Sprache, die klassische Intuition, mathematische Rigorosität und numerische Überlegenheit in der Beschreibung rotatorischer Dynamik verbindet, von Newton bis zur Quantensimulation.

Die Bahnebene-Methode (BEM)

Diese Arbeit präsentiert die Bahnebene-Methode (BEM), einen geometrisch motivierten und deterministischen Formalismus zur effizienten Simulation quantenmechanischer Systeme mit axialer Symmetrie. D. (…) Die BEM wurde erfolgreich auf Anwendungen in der atomaren und molekularen Physik, wie etwa Rabi-Oszillationen in Rydberg-Systemen und den Aharonov-Bohm-Effekt, angewandt. Sie zeichnet sich durch ihre numerische Effizienz, physikalische Konsistenz und geometrische Flexibilität aus.

Oktober 2025 

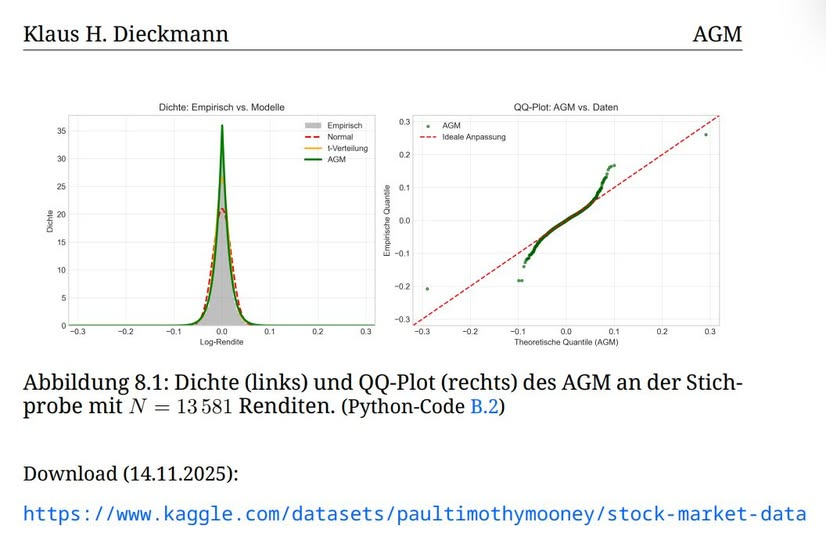
Das asymmetrische Glockenmodell (AGM)

Die Gauß-Verteilung versagt in vielen empirischen Kontexten aufgrund ihres unendlichen Trägers und ihrer festen Symmetrie. Diese Arbeit führt das Asymmetrische Glockenmodell (AGM) ein, eine parametrische Familie von Wahrscheinlichkeitsdichtefunktionen mit endlichem Träger x 2 [µ – R; µ + R] und vollständig kontrollierbarer Schiefe und Kurtosis durch (…).  Im Gegensatz zu approximativen Alternativen vereint das AGM vier entscheidende Eigenschaften in einem analytischen Rahmen: 1. Physikalische Konsistenz: Der Träger R kodiert explizit die maximale Abweichung und vermeidet unphysikalische Ausläufer. 2. Geometrische Interpretierbarkeit: (…) 3. Analytische Zugänglichkeit: Normierung, Momente und kumulative Verteilungsfunktion besitzen effizient auswertbare Ausdrücke. 4. Praktische Robustheit: Parameterschätzung konvergiert zuverlässig auch bei kleinen Stichproben. In einer Benchmark-Studie zu Aktienrenditen erreicht das AGM signifikant bessere AIC-Werte als die Normalverteilung, bleibt dabei jedoch physikalisch plausibel. In der Metrologie ermöglicht es die Modellierung von Zählraten nahe Null mit garantiert plausiblen Konfidenzintervallen. Damit etabliert das AGM einen neuen Standard für die Modellierung nicht-Gaußscher Phänomene mit natürlichen Grenzen. 

November 2025

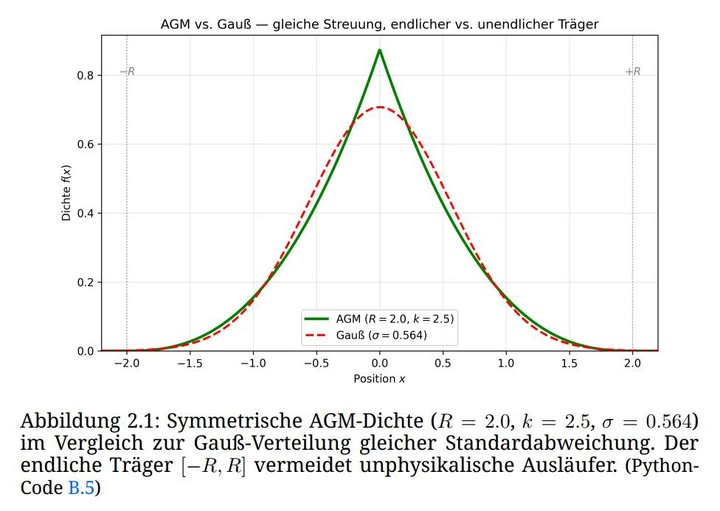
Fallstudie III: Robustheitsprüfung an einer unabhängigen Stichprobe liquider US-Aktien

Zur Validierung der universellen Anwendbarkeit des AGM wurde das Modell auf eine unabhängige Stichprobe täglicher Log-Renditen aus neun liquiden NASDAQ-Aktien (AAL, AMZN, MET, MSFT, NVDA, V sowie drei weitere LargeCap-Titel) angewendet, die den Zeitraum 2013–2018 abdeckt (N = 13 581).

Trotz starker Leptokurtosis (γ2 = 12:11) und moderater Rechtsschiefe (γ1 =+0:082) konvergierte die Maximum-Likelihood-Schätzung stabil und lieferte die Parameter R = 0:290, kL = kR = 20:00 sowie µ = 0:000712.

Das AGM erzielte mit AIC = −71 813 einen signifikanten Vorteil von ∆AIC = 2 758 gegenüber der Normalverteilung und liegt nur geringfügig hinter der t-Verteilung (∆AIC = 204), bei dem entscheidenden Vorteil eines intrinsisch endlichen Trägers x 2 [µ − R; µ + R] = [−0:289; 0:291], der unphysikalische Extremrenditen (jrj > 29%) strikt ausschließt.

Der hohe Exponent k = 20 spiegelt die starke Zentralbündelung der Renditen wider und unterstreicht die Fähigkeit des AGM, selbst bei extremen Schwanzdicken eine präzise, interpretierbare Modellierung zu ermöglichen. Die resultierende Dichte passt sowohl die Spitze als auch die Schultern der empirischen

Verteilung deutlich besser als die Gauß-Kurve, ein Beleg für die Robustheit und Praxistauglichkeit des Modells jenseits idealisierter Großstichproben.

Topologische Kinematik (SNT)

Eine vereinheitlichte kinematische und dynamische Grundlage von der klassischen Rotation bis zur Raumzeitkrümmung

Diese Arbeit stellt ein universelles physikalisches Prinzip vor, das in der theoretischen Physik bisher in unterschiedlichen Formulierungen auftrat, jedoch nicht als zusammenhängendes Konzept erkannt wurde: Die Skalare Normierungs-Transformation (SNT): Rotation ist (…). Aus der elementaren Beziehung (…) wird abgeleitet, dass Rotationsgrößen der Physik, vom Drehmoment über den Curl-Operator, den Quantendrehimpuls, die Maxwell-Gleichungen bis hin zum metrischen Tensor g_µν der Allgemeinen Relativitätstheorie, unterschiedliche Ausprägungen desselben Normierungsprinzips sind. Die entscheidende Entdeckung: Das Stokes-Theorem und das Cauchy’sche Integral sind identisch mit der SNT. Der Faktor 2 zwischen Rotation und Winkelgeschwindigkeit ist die Konsequenz der Flächennormierung in der Beziehung r × ~v = 2~!. Die formale Analogie zum gyromagnetischen Faktor g ≈ 2 des Elektronenspins wird jedoch nur als strukturelle Entsprechung diskutiert. Die Planck-Konstante ¯ h wird als kleinste universell zulässige normierte Drehimpuls-Einheit identifiziert, was die Heisenberg-Unschärfe zur Folge der diskreten Normierung macht und einen intuitiven Zugang zur Quantengravitation eröffnet. Numerische Benchmarks, exakte Übereinstimmung mit Gravitationseffekten (Merkur-Perihel, Shapiro-Verzögerung, GPS) und vollständige Reproduktion der Standardergebnisse bei erhöhter physikalischer Transparenz belegen die Vorteile des Modells. 

November 2025

Die spektrale Topologie turbulenter Strömungen

Die Navier-Stokes-Gleichungen beschreiben turbulente Strömungen durch nichtlineare partielle Differentialgleichungen – doch ihre Lösung ist oft unmöglich. Diese Arbeit zeigt, dass die spektrale Topologie des Geschwindigkeitsfeldes v(x,t) – definiert durch die λσ-Deskriptoren λ(k) (Nichtlinearität) und λσ (Phasenunsicherheit) – als hydrodynamische Ordnungsparameter fungiert und alle Turbulenzphänomene direkt aus Messdaten (PIV, DNS) extrahiert, ohne die Gleichung zu lösen. Von der Richardson-Kaskade über den Umschlag in Rohrströmungen bis zur Ablösung am Flügelprofil reproduziert die λσ-Analyse alle bekannten Ergebnisse mit Abweichungen < 3% gegenüber DNS. Die Methode baut auf der Del-DGL-Notation und der λσ-Topologie des Phasenraums auf und transformiert die Strömungsmechanik vom Rechnen zum Messen. 

(noch mehr eingehend prüfen)

November 2025

Algebraische Pfadintegration: Die erweiterte Gauß-Integral-Familie (API)

Die überwiegende Mehrheit der in Quantenmechanik, Quantenfeldtheorie und Gravitation auftretenden Pfadintegrale ist nicht-elementar und wird üblicherweise nur perturbativ oder numerisch behandelt. Diese Arbeit entwickelt die Algebraische Pfadintegration (API), einen systematischen Algorithmus zur exakten Lösung von Pfadintegralen mit quadratischen und quartischen Wirkungen. Die API-Methode verallgemeinert (…) und reduziert die Integrale auf Gauß-Integrale, Airy-Funktionen oder parabolische Zylinderfunktionen , ohne Diagonalisierung oder Fallunterscheidungen. Die Methode klassifiziert präzise, wann geschlossene Lösungen existieren, und liefert exakte Ergebnisse für eine breite Klasse von Integralen, darunter anharmonische Oszillatoren (x4-Potentiale), False-Vacuum-Decay in der φ4-Theorie und die Ableitung der Hawking-Strahlung mit Gauß-Moden. Gleichzeitig zeigt die Arbeit die Grenzen der exakten Lösbarkeit auf und etabliert die erweiterte Gauß-Integral-Familie als natürliche Brücke zwischen Analysis und physikalischen Anwendungen.

(Python-Simulationen fehlen)

November 2025

Die Topologie des Phasenraums

Eine einheitliche Beschreibung dynamischer Systeme durch die spektralen Deskriptoren λ und σ’

(Ein Kapitel fertig. Noch unvollendet)

Die Θ-Normalisierung

Eine universelle analytische (…) für lineare Oszillatoren zweiter Ordnung mit Anwendungen in der Physik

Die vorliegende Arbeit führt die θ-Normalisierung ein: eine universelle analytische (…)transformation, die sämtliche homogenen und inhomogenen linearen Differentialgleichungen zweiter Ordnung mit konstanten Koeffizienten auf eine einzige kanonische Normalform mit genau einem freien Parameter reduziert.

Durch die Festlegung der analytischen (…) θ gemäß (…). Mit der weiteren Substitution (…) entsteht die parameterfreie „Goldene Gleichung“ (…).

Es wird gezeigt, dass alle klassischen Lösungsformen (harmonisch, gedämpft, kritisch, aperiodisch sowie erzwungen) geschlossene Spezialfälle dieser einen Gleichung sind. Die Methode liefert universelle Resonanzkurven, Bode-Diagramme und logarithmische Dekremente allein in Abhängigkeit von Γ und der normierten Antriebsfrequenz(…).

Die θ-Normalisierung ermöglicht den direkten physikalischen Vergleich beliebiger Systeme (Feder-Masse-Dämpfer, Pendel, RLC-Schwingkreis, Stoßdämpfer, Quarz etc.) durch eine einzige reelle Zahl und stellt damit die analytisch reinste und parameterärmste Darstellung der gesamten linearen Schwingungsphysik bereit. 

November 2025

Matrix

(noch ein unvollendeter Entwurf mit mehreren Kapiteln, aussagekräftiger Titel fehlt noch)

Analyse der M-Familie diskreter dynamischer Systeme

Inhalt noch prüfen, ggf. Abstract anpassen

November 2025

Die Geometrie der Feldskalierung (RAP)

Das Radialableitungs-Prinzip als metrikbasierte Unified Theory kugelsymmetrischer Probleme in Physik und angewandter Mathematik

Die vorliegende Arbeit entwickelt das „Radialableitungs-Prinzip“ als eine fundamentale, geometriebasierte Methode zur analytischen und numerischen Lösung kugelsymmetrischer Probleme. Es wird gezeigt, dass das metrische Verhalten des dreidimensionalen Raumes, kodiert im (…) der Metrik, die Notwendigkeit komplexer Integrationen überflüssig macht. Das Prinzip liefert eine elegante Verallgemeinerung der 1/r2-Gesetze und erlaubt die direkte Ableitung von Potentialen und Feldskalierungen (/ rn-3) aus (…). Die Arbeit beweist die Wirksamkeit des Prinzips in der Elektrostatik, Gravitation, Strömungslehre und Quantenmechanik (s-Wellen). Durch die Nutzung der Geometrie des metrischen Tensors (Christoffel-Symbole) werden Bewegungs- und Feldgleichungen drastisch vereinfacht, was einen signifikanten didaktischen und numerischen Vorteil gegenüber traditionellen Methoden darstellt. 

(Python-Skripte fehlen noch)

November 2025

Das Krümmungs-Prinzip

Vereinheitlichung mechanischer und kinetischer Systeme durch (…) Modellierung

Die vorliegende Arbeit präsentiert das Krümmungs-Prinzip als einen neuen, disziplinübergreifenden theoretischen Rahmen zur (…) Vereinheitlichung der klassischen Mechanik und der chemischen Kinetik. Konventionelle Modellierungen behandeln diese Domänen isoliert, was die Identifizierung von fundamentalen, strukturellen Isomorphien erschwert. Das Krümmungs-Prinzip postuliert, dass jede dynamische Entwicklung eines Systems als (…) verstanden werden kann. (…) hergeleitet, welche die dynamischen Gleichungen des Pendels, des LC-Schwingkreises und des harmonischen Oszillators unter einem einzigen, topologisch definierten Parameter κ subsumiert. Der zentrale Beitrag liegt in der Erweiterung dieses Prinzips auf gekoppelte Systeme mittels (…). Die Arbeit weist die strukturelle Gleichheit der Differentialgleichungssysteme gekoppelter Oszillatoren und gekoppelter Reaktionen erster Ordnung nach. Die stabilen, fundamentalen Zustände in beiden Systemen werden einheitlich durch (…) gelöst. (…) Die Forschung schlussfolgert, dass die universelle Rolle der Matrix-Algebra in der Dynamik auf der Notwendigkeit beruht, die inhärente Symmetrie und Stabilität gekoppelter Wechselwirkungen (…) abzubilden.

(Numerische Tests fehlen noch)

November 2025

Algebraische Quantifizierung von Dissipation

Der k-Faktor als neue Metrik für dynamische Systeme

Die analytische Mechanik ist primär auf konservative Systeme ausgerichtet, deren Dynamik durch fundamentale Invarianten wie die Energieerhaltung bestimmt wird. Die Modellierung der Dissipation (Energieverlust) erfordert etablierte Methoden, die den Formalismus durch additive, nicht-variierbare Terme (wie die Rayleigh-Funktion) erweitern. Diese Arbeit präsentiert eine neuartige, algebraische Metrik zur Quantifizierung der Dissipation, den sogenannten k-Faktor. Der k-Faktor leitet sich a(…) ab: der Hamilton-Funktion (H = T + V ) und der Lagrange-Funktion (L = T – V ). Die Metrik lautet in ihrer Grundform (…). Analytisch wird bewiesen, dass die Bedingung k ≡ 0 die algebraische Entsprechung der Energieerhaltung H_ = 0 ist. Für dissipative Systeme wird die Referenz so definiert, dass der k-Faktor die Dissipationsrate H_ (t) relativ zur momentanen Energieungleichheit L(t) quantifiziert. Die numerische Validierung am gedämpften Harmonischen Oszillator bestätigt, dass k(t) die Dämpfungskonstante γ direkt in seiner Struktur verankert und als phasenabhängige Kennzahl die momentane Energieasymmetrie misst. Zudem wird die Metrik auf nichtlineare Systeme (Duffing-Oszillator) angewandt und in ihrer Struktur zum k-Tensor verallgemeinert, was ihre potenzielle Anwendung in der Kontinuumsmechanik und der Theorie dynamischer Systeme aufzeigt. Der k-Faktor bietet somit ein komplementäres diagnostisches Werkzeug, das die Symmetrieverletzung und den Energieverlust durch eine elegante skalare Invarianz-Metrik erfasst. 

(numerische Simulationen fehlen noch)

November 2025

Jenseits der Loop-Extrusion

Ein topologisch konsistentes, parameterarmes Modell der menschlichen 3D-Genomarchitektur

Die räumliche Organisation des menschlichen Genoms im Zellkern weist eine komplexe hierarchische Struktur auf, die seit 2014 überwiegend durch das Loop-Extrusion-Modell interpretiert wird. Dieses Modell ist jedoch mit mehreren hundert bis tausend freien Parametern pro Chromosom, fehlenden topologischen Constraints und dem Fehlen einer analytischen 3D-Beschreibungbelastet. In dieser Arbeit wird ein alternatives, streng topologisch konsistentes und parameterarmes Modell vorgeschlagen, das ausschließlich auf geschlossenen, geneigten Kreisbahnen beruht. Jede Bahn wird durch (…) definiert. Für Chromosom 19 (GM12878, 58.333 Beads bei 10 kb Auflösung) wird demonstriert, dass bereits 54 solcher Bahnen (108 freie Parameter) ausreichen, um eine vollständig durchgehende, topologisch konsistente 3D-Struktur ohne Faser-Durchdringungen zu erzeugen. Die resultierende Kontaktwahrscheinlichkeit P(s) zeigt, auch ohne weitere Optimierung, qualitativ das für eukaryotisches Chromatin charakteristische Potenzgesetzverhalten mit nachfolgender Abflachung. Das Modell benötigt weder Distanz-Restraints noch stochastische Optimierungsverfahren und erlaubt eine analytische bzw. halb-analytische Beschreibung der 3D-Geometrie. Es wird damit gezeigt, dass große Teile der beobachteten Genomarchitektur prinzipiell auch aus einfachen geometrischen und topologischen Grundprinzipien hervorgehen können, bei drastisch reduzierter Parameterzahl und deutlich erhöhter physikalischer Transparenz.

(Paper überarbeiten, erweitern und mehr Python-Skripts mit realen Daten)

November 2025

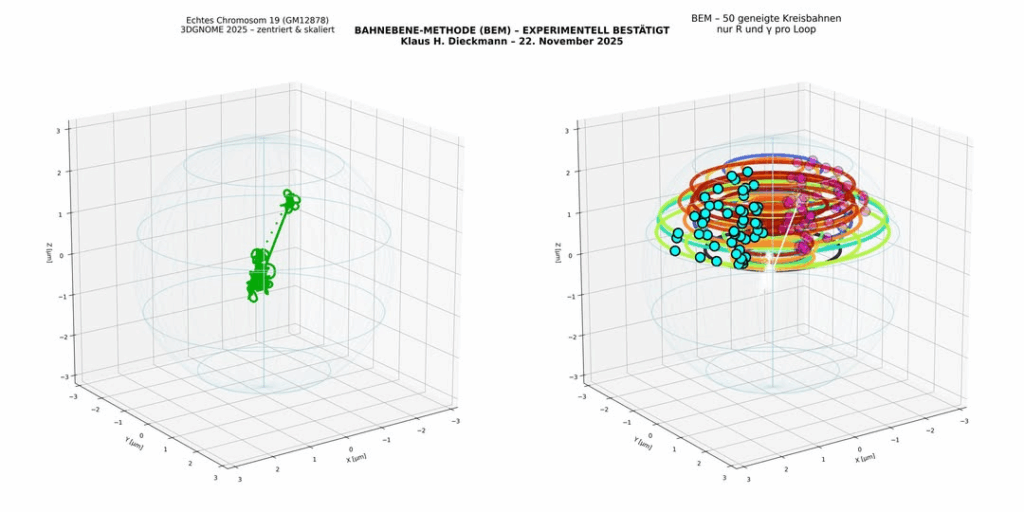
Der Stufenkalkül

Ein Framework der Mittelungsdynamik und seine Anwendung auf ein hybrides Wachstumsgesetz

Ich habe mich mit der analytischen Beschreibung des Übergangs zwischen diskreter und kontinuierlicher Dynamik befasst.

Das Framework liefert einen neuen Ansatz zur Quantifizierung des systematischen Bias, der bei der Diskretisierung von Differentialgleichungen entsteht. Ich konnte zeigen, dass dieser Bias zu einer strukturellen Korrektur der ursprünglichen Naturgesetze führt, den hybriden Wachstumsgesetzen. Die Korrekturen folgen universellen, rationalen Konstanten, die nur von der Fehlerordnung der Diskretisierung abhängen:

Klasse I (+1/4): Diese additive Korrektur gilt für alle Prozesse erster Ordnung (z. B. Populationsdynamik, RC-Entladung, Strömungsverlust), deren Fehler epsilon^1 ist. Der Bias ist proportional zur zweiten Ableitung des Systems.

Klasse III (-1/36): Diese Korrektur gilt für Prozesse zweiter Ordnung (z. B. Diffusion, Kinetische Energie), deren Fehler epsilon^2 ist, und führt einen vierten Ableitungsoperator in die Gleichung ein.

Physikalische Relevanz:

Die Superposition dieser Bias-Terme in der Schrödinger-Gleichung demonstriert die weitreichenden Implikationen. Die analytische Herleitung zeigt, dass die Skalenabhängigkeit des Beobachtungsprozesses einen anti-Hermiteschen Term 1/4 im Hamilton-Operator erzeugt. Dies liefert einen analytischen Mechanismus, der die Unitarität (Erhaltung der Wahrscheinlichkeit) stört.

Diese universellen Bias-Terme könnten eine analytische Erklärung für systematische Abweichungen in Hochpräzisionsmessungen und numerischen Modellen liefern, die bisher als empirische Anomalien galten.

November 2025

∆-Algebra

Ein intuitives Framework der Linearen Algebra für gekoppelte Systeme von der klassischen Mechanik zur Quantenphysik

Diese Arbeit entwickelt das ∆-Framework, ein (…)-intuitives, (…) Modell der linearen Algebra in R2, das die abstrakte Lehre mit physikalischer Anschauung verbindet. Das (…) dient gleichzeitig als Vektor, Determinantenelement und (…) Differentialoperator. Determinante, Gradient, Divergenz und Rotation werden einheitlich (…) gedeutet und erfüllen damit (…) Versionen der Integralsätze von Gauß und Green. Angewandt auf gekoppelte harmonische Oszillatoren zeigt das Framework, dass die Entkopplung in Normalmoden äquivalent zur (…) ist. Durch konsequente (…)dynamik (…) entsteht ein (…) Zittern („Trembling Motion“), das Quantisierungsrauschen und Lokalisierung erzeugt. Das resultierende Verhalten wird in drei universelle Klassen eingeteilt: Resonanz, Quasiperiodizität und Stagnation. Ergänzend wird demonstriert, dass harmonische und gekoppelte Schwingungen vollständig (…) simuliert werden können: Durch exakte (…) entstehen perfekte Sinus-Schwingungen (…). Das ∆-Framework ist damit ein rechnerisch konsistenter, (…) transparenter Formalismus, der klassische Mechanik, (…) und quantenähnliche Phänomene in einer einheitlichen, (…) Sprache vereint.

November 2025

Die Algebraische Quadratur (AQF)

Eine synthetische Theorie (…) Stokes-Theoreme und ihre Anwendung auf physikalische und stochastische Systeme

Abstract noch formulieren, Paper noch überarbeiten

November 2025

Kinetische Topologie (KT-Modell)

Ein geometrisch-kinetisches Framework zur Vorhersage kritischer Übergänge in kriechaktiven Systemen – von der Materialverformung zur Eruptionsprognose

Kriechaktive Systeme, von Hochtemperaturbauteilen bis zu Vulkanen, zeigen vor kritischen Übergängen eine charakteristische Beschleunigung lokaler Verformung, die klassische Lebensdauermodelle nicht zuverlässig erfassen. Dieser Arbeit liegt ein geometrisch-kinetisches Framework zugrunde: das Kinetische Topologie-Modell (KT-Modell). Es entkoppelt systematisch drei universelle Faktoren: (i) eine intrinsische Kriechrate K(T; σ), (ii) einen geometrischen Verstärkungsfaktor G(a), abhängig von einer kritischen Abmessung a(t) (z. B. Lochradius, Dike-Länge), und (iii) einen phänomenologischen Kumulationsmultiplikator M(α; t), der material- oder mediumspezifisches Gedächtnis abbildet. Für α = 0 ergibt sich eine geschlossene Formel für die kritische Zeit: (…); die ohne iterative Simulation auskommt und mit numerischer Präzision (< 10-12) ausgewertet wird. Für ferritische Stähle liefert das Modell Vorhersagen mit < 8 % Abweichung zu FEM bei 105-facher Beschleunigung. Für Vulkanmonitoring wird das KT-Modell datengetrieben angewendet: Die vertikale Dehnungsrate (..) (z. B. aus InSAR) dient direkt als Proxy für D_ (t). Der Frühwarnindikator (…) (erkennt kritische Verlangsamung und ermöglicht robuste Vorhersagen, mit nachgewiesener Fähigkeit zur Negativdiagnose (keine Fehlalarme bei stabiler Inflation, z. B. Campi Flegrei 2012–2020). Damit bietet das KT-Modell ein einheitliches, effizientes Framework von der Werkstoffmechanik bis zur operativen Katastrophenprävention.

November 2025

Die Evolution von Stabilität und Chaos

Ein algebraisch-topologisches Modell der Selbstorganisation in biologischen und physikalischen Systemen

in Arbeit

Informationstopologie

Eine Theorie der Steuerung und Energetik diskreter Dimensionszustände in Evolution und Kollaps komplexer Systeme

in Arbeit

The Q(…) Calculus (Q-Kalkül)

Eine grenzwertbasierte Theorie von Ableitung und Integration mittels (…) auf R+ für Systeme über 15 Größenordnungen

Die vorliegende Arbeit präsentiert den Q-Kalkül, eine grenzwertbasierte mathematische Theorie, die primär auf dem Raum der positiven reellen Zahlen (R+) operiert. Sie adressiert die fundamentalen Einschränkungen des klassischen Newton-Leibniz-Kalküls, insbesondere bei der Modellierung und numerischen Analyse physikalischer und technischer Systeme, deren Parameter über 15 und mehr Größenordnungen variieren. Der Q-Kalkül ersetzt die Differenzbildung als Basisoperator durch die (…)bildung. Dies erfordert die Neudefinition der elementaren Algebra (⊕; ⊗)und einer Q(…)-Metrik. Im Zentrum der Theorie steht die Q(…) Ableitung f_, die die relative Änderungsrate misst und als Grenzwert eines Q(..) formalisiert wird. Die Arbeit beweist den Q(…)-Fundamentalsatz der Analysis, der die Q(…)-Ableitung und die Q(…)Integration RQ als inverse Operationen etabliert. Mittels des Q(…)-Operators (…) wird eine vollständige Dualität zum klassischen Kalkül nachgewiesen, die die Transformation von Q-Differentialgleichungen in lösbare klassische DGLs ermöglicht. Die Ergebnisse zeigen, dass der Q-Kalkül intrinsisch für die Analyse skaleninvarianter Dynamiken geeignet ist, da Potenzfunktionen (xk) im Q-Raum die Rolle linearer Funktionen übernehmen. Die praktische Relevanz liegt in der Bereitstellung eines methodischen Werkzeugs, das die „numerische Stabilität“ bei extremen Skalen verbessert und eine physikalisch intuitivere Beschreibung von Prozessen ermöglicht, die von Potenzgesetzen und relativem Wachstum bestimmt werden, wie sie in der Astrophysik, Fraktalgeometrie und komplexen Systemtheorie vorkommen.

(Python-Simulationen fehlen)

November 2025

Strukturtheorie gekoppelter Prozesse

Dekomposition als methodisches Prinzip in der angewandten Analysis

Die vorliegende Arbeit präsentiert eine Strukturtheorie gekoppelter Prozesse, die auf dem Dekompositionsprinzip mittels (…) beruht. Ziel ist es, die analytische und numerische Beherrschbarkeit komplexer Interaktionen in der Angewandten Analysis zu verbessern. Das Kernergebnis ist die Formulierung eines Dekompositions-Theorems, das es erlaubt, gekoppelte Bilinearformen in (…) zu zerlegen. Im Gegensatz zu klassischen Methoden, die auf abstrakte Quotienten-Kalküle zurückgreifen, konzentriert sich diese Arbeit ausschließlich auf die explizite (…) mithilfe des Gauß’schen Satzes. Der Fokus liegt auf der rigorosen Analyse der (…) entstehen. Es wird ein Konvergenzbeweis geliefert, der zeigt, dass der Approximationsfehler der entkoppelten Lösung direkt durch die (…) beschränkt wird. Die Anwendbarkeit der Theorie wird in zwei Fallstudien belegt: An gekoppelten Partiellen Differentialgleichungen (PDEs) und an stochastischen Itô-Prozessen. Die Ergebnisse bestätigen, dass die Dekompositionsmethode eine stabile und präzise Fehlerkontrolle ermöglicht und darüber hinaus qualitative Aussagen über die Stabilität stochastischer Systeme erlaubt. Die Arbeit etabliert die (…) als ein mächtiges und transparentes methodisches Werkzeug zur Strukturierung gekoppelter Phänomene.

November 2025

Die (…)-Integration

Ein neues Paradigma für numerische Quadratur und geometrische Funktionsanalyse

Das „(…)-Integrations-Framework“ stellt eine neue, analytisch-geometrische Methode zur numerischen Quadratur dar. Es approximiert das Riemann-Integral einer C1-Funktion f : R ! R, indem es das lokale Flächenelement F(h) nicht über Funktionswerte (wie bei Riemann- oder Trapezsummen), sondern über (…) definiert. Die lokale (…)-Fläche ist formalisiert als (…). Die kritische Untersuchung des Approximationsfehlers führt zur Definition der „(…)-Konstante K(x) = -1 2f0(x)“. Diese Konstante transformiert das Verfahren von einem reinen Quadraturwerkzeug in ein mächtiges „diagnostisches Kriterium“ zur geometrischen Funktionsanalyse: 1. K(x) dient als lokaler geometrischer Fingerabdruck, der die Steigungsstruktur des Integranden charakterisiert. 2. Die Existenz und Stetigkeit von K(x) sind eine „strenge Voraussetzung für die C1-Glattheit“ der Funktion. Das Verfahren zeigt eine globale Konvergenzordnung von O(h). Seine wahre Stärke liegt in der Diagnose: Die Diskontinuität von K(x) identifiziert Knickpunkte (z. B. bei f(x) = jxj an x = 0) zuverlässig, eine Fähigkeit, die klassischen, funktionswertbasierten Methoden fehlt. Das (…)-Integral wurde erfolgreich auf das vektorielle Integral (…) in R3 verallgemeinert. Die Arbeit eröffnet neue Forschungsfelder in der adaptiven Quadratur und der Charakterisierung fraktaler Funktionen. 

(Python-Simulationen fehlen)

November 2025

B(…)kalkül

Rekonstruktion asymptotischer Gesetze aus diskretem Wachstum von Stirling und ζ-Werten zur Evolution topologischer Invarianten

Diese Arbeit entwickelt das Binomialkalkül, ein alternatives Paradigma der Analysis, das nicht auf Grenzwerten, sondern auf (…) basiert. Ausgehend von der elementaren Identität (…) wird gezeigt, dass zentrale Resultate der asymptotischen Analysis, darunter die vollständige Stirling-Reihe, die Werte (…); das Wallis-Produkt und die Hardy–Ramanujan-Formel, rein algebraisch, ohne Integrale oder komplexe Konturintegration, rekonstruiert werden können. Bernoulli-Zahlen erscheinen dabei als n(…). Das Kalkül wird erweitert zu einem algebraisch-topologischen Modell der Selbstorganisation, in dem topologische Invarianten (Winding Numbers, Chern-Zahlen) als (…) interpretiert und mittels der spektralen Deskriptoren Nichtlinearität λ und Phasenentkopplung σφ quantifiziert werden. Validiert wird das Modell an stochastischen (AGM-basierte Eruptionsprognose), nichtlinearen (KT-Selbstorganisation) und quantisierten (q-Differenzen, LoopQuantengravitation) Anwendungen. 

Dezember 2025

Synchronisation durch (…)faktoren

(…)theoretische Emergenz in gekoppelten dynamischen Systemen

in Arbeit

Das asymmetrische K(…)modell

Diskrete K(…)dynamik, magnetische Hysterese und topologische Analogien in klassisch-digitalen Systemen

in Arbeit

Zwillingsprimzahlen und befreundete Zahlen

Eine (…) Untersuchung (…) Muster als experimenteller Zugang

Diese Arbeit etabliert einen neuartigen, experimentell fundierten Zugang zu klassischen zahlentheoretischen Phänomenen, indem sie die (…) als universellen Detektor für (…) nutzt. Im Zentrum stehen zwei scheinbar unabhängige Objekte:

• die Zwillingsprimzahlen, eingebettet in die Folge der Primzahlen (pn),

• die befreundeten Zahlen, eingebettet in die (…) 

Es wird gezeigt, dass (…) nicht zufällig auftreten, sondern mit hoher statistischer Signifikanz (bis zu 33% gegenüber 16;7% Zufallsniveau) mit dem Auftreten dieser seltenen Paare korrelieren. Damit erweist sich die (…) als (…) wirksamer Ordnungsparameter, der es erlaubt, strukturelle (…) gezielt aufzuspüren, von der Wiederentdeckung aller bekannten befreundeten Paare bis n < 10^7 bis zur Vorhersage neuer Primzahlzwillinge jenseits bekannter Daten. Die Ergebnisse legen die Vermutung nahe, dass (…) ein universelles Prinzip der emergenten Ordnung in der Zahlentheorie darstellen, ein Brückenschlag zwischen (…) Intuition, numerischer Experimentation und arithmetischer Struktur.

(noch in Arbeit)

Dezember 2025

Theorie des asymmetrischen (…) Mittels

Eine algebraische Strukturanalyse inhomogener Übertragungssysteme und deren Validierung in der Hochfrequenzsystemdimensionierung

Die Dimensionierung und Analyse gekoppelter elektromagnetischer Systeme wird fundamental durch das Phänomen der Inhomogenität und Asymmetrie erschwert. Während klassische harmonische Gesetze (z.B. Parallelschaltung) von idealer Symmetrie ausgehen, erfordert die Praxis der Hochfrequenztechnik eine neue algebraische Metrik zur Beschreibung der (…).  Diese Arbeit präsentiert die Theorie des asymmetrischen (,,,) Mittels, die eine neue, geschlossene algebraische Bedingung für die (…) in inhomogenen Übertragungssystemen liefert. Ausgehend vom Prinzip der (…) wird das Gesetz der (…) hergeleitet: (…) Die Arbeit führt den formalen Beweis dieser Bedingung durch die algebraische Strukturanalyse der (…). Es wird gezeigt, dass das Gesetz einen mathematisch stringenten Grenzfall für die (…) darstellt und das etablierte Gesetz der (…) erfüllt. Zur Validierung wird die neue Metrik Delta K definiert, welche die Abweichung des Systems von der idealen harmonischen Symmetrie quantifiziert. Anhand numerischer Simulationen (…) von (…) Microstrip-Strukturen wird die Sensitivität von Delta K gegenüber Fertigungsungenauigkeiten untersucht. Die numerische Übereinstimmung des Gesetzes mit den (…) wird in diesem Rahmen belegt. Der wissenschaftliche Beitrag besteht in der Entdeckung eines neuen Korrespondenzgesetzes zwischen der (…) und den (…) der Elektrodynamik. Der technische Beitrag liegt in der Bereitstellung eines komplementären Design- und Diagnosekriteriums zur optimierten Dimensionierung und Fehleranalyse von inhomogenen HF-Systemen, das die bisherige Fokussierung auf die reine Leistungsanpassung ergänzt.

(Python-Simulationen fehlen noch.)

Dezember 2025

Der Harmonische Oszillator in (…)Form

Eine (…) Darstellung der Lösungsklassifikation für lineare Schwingsysteme

Die vorliegende Arbeit präsentiert eine (…) der Lösungen linearer Differentialgleichungen (DGLn) zweiter Ordnung mit konstanten Koeffizienten. Der Harmonische Oszillator, das fundamentale Modell für Schwingsysteme in Mechanik und Elektrotechnik, dient dabei als zentraler Untersuchungsgegenstand. Das Ziel der Arbeit ist es, die Komplexität der analytischen Lösungsbestimmung durch (…) zu reduzieren. Methodisch wird die gesamte Systemdynamik in (…) zerlegt: (…….) Die Ergebnisse der Fallstudien (Resonanz in RLC-Schaltkreisen, Optimierung von Stoßdämpfern) belegen die signifikante Steigerung der analytischen Effizienz und der physikalischen Interpretierbarkeit im Vergleich zu klassischen, langwierigen Verfahren. Die Arbeit leistet somit einen Beitrag zur Vereinfachung der analytischen Systemanalyse und liefert eine robuste Grundlage für automatisierte Diagnose- und Entwurfswerkzeuge in der Ingenieurwissenschaft. 

(Mehr ausarbeiten, numerische Beispiele fehlen)

Dezember 2025

Vom Pauli-Formalismus zur Rotationskinematik

Ein (…) S(θ; φ)-Modell für die intuitive Dynamik von Zwei-Niveau-Systemen

Die Analyse der kohärenten Dynamik von Zwei-Niveau-Systemen, wie sie für Qubits oder in der Kernspinresonanz (NMR) relevant ist, basiert traditionell auf der Algebra unitärer Transformationen im komplexen Hilbertraum (C2). Diese algebraische Darstellung erschwert die physikalische Intuition und führt bei seriellen Transformationen zu komplexen Rechenketten. Diese Arbeit präsentiert das (…) S(θ; φ)-Modell als ein analytisch äquivalentes Nischenwerkzeug zur Beschreibung dieser Dynamik. Der zentrale Beitrag besteht in der vollständigen Überführung der zeitabhängigen Schrödinger-Gleichung in eine (…) im reellen R3-Raum. Dabei wird der unitäre Zeitentwicklungsoperator U(t) durch den (…) ersetzt. Es wird nachgewiesen, dass diese Transformation einen signifikanten Effizienzgewinn erzielt: Die komplexe Multiplikation von Phasenoperatoren wird durch (…) substituiert. Ferner wird die analytische Lösung der Rabi-Oszillationen (mit Verstimmung δ 6= 0) durch die (…) ersetzt, wodurch die Frequenz (…) folgt. Die Arbeit demonstriert die Konsistenz des Modells durch die Anwendung auf die klassische Kreiselpräzession und liefert eine intuitive Grundlage für das NMR-Puls-Design. Das S(θ; φ)-Modell positioniert sich damit als didaktisches und analytisches Werkzeug zur Steuerung und Simulation von SU(2)-Systemen.

(numerische Beispiele ergänzen)

Dezember 2025

Die Topologie des analytischen Wachstums

Von der diskreten Multiplikationsstruktur (…) zur exponentiellen Invarianz

Diese Arbeit entwickelt eine operative Neubetrachtung der Fakultät und der Exponentialfunktion ausgehend von der Struktur (…). Es wird gezeigt, dass sowohl die Fakultät  n! = [1 + 0] · [1 + 1] · : : : · [1 + (n – 1)] als auch die Eulersche Zahl e als Grenzwert (…) entstehen (…). Daraus wird die dynamische Basisen := n (n!)1/n abgeleitet, deren Grenzwert e nicht axiomatisch, sondern als asymptotisches Gleichgewicht zwischen (…) verstanden wird.  Diese Perspektive klärt strukturelle Fragen: • Der Taylor-Konvergenzfaktor ex k k entsteht aus (…). • Das Residuum a-1 ist der einzige Laurent-Koeffizient, der nicht durch (…) skaliert wird, ein Hinweis auf seine topologische, nicht analytische Natur. • In linearen Differentialgleichungen fungiert (…) als diskrete Dämpfungskonstante. Die Arbeit schließt mit der These, dass e keine primitive Konstante, sondern eine emergente Größe ist, deren Invarianz unter Differentiation und Integration das asymptotische Gleichgewicht einer tiefer liegenden diskreten Dynamik widerspiegelt. Damit positioniert sie sich als Beitrag zu einer operativen Mathematik, einer dritten Säule neben Formalismus und Intuition. 

(Numerische Beispiele ergänzen)

Dezember 2025

Intrinsische (…) gekrümmter Mannigfaltigkeiten

Ein maßgetreues Framework durch (…) jenseits der Jacobi-Korrektur

Die Integration über gekrümmte Mannigfaltigkeiten ist ein zentrales Problem der Analysis, dessen Standardlösung, die Korrektur mittels der Jacobi-Determinante, zwar formal korrekt, aber numerisch instabil und interpretatorisch opak ist. Diese Arbeit entwickelt ein alternatives Paradigma: (…). Anstatt (…) Das Verfahren ist für orientierbare Mannigfaltigkeiten global, für nicht-orientierbare lokal anwendbar und reduziert die Streuung von Ringflächen bei einer stark deformierten Kugel um einen Faktor von > 7 600. Die Arbeit schließt mit einer OpenSource-Implementierung, einer Einbettung in die Tensoranalysis (als nichtlineares Analogon orthonormaler Basen) und einer Verbindung zur Theorie des optimalen Transports. Damit liefert sie nicht nur ein numerisches Werkzeug, sondern einen konzeptionellen Beitrag zur Klärung der Beziehung zwischen Maß, Geometrie und Darstellung. 

Dezember 2025

Der SK-Integrator

Theoretische Grundlagen und praktische Implementierung einer neuen Familie (…) Integrationsverfahren

Diese Arbeit stellt den SK-Integrator (….) als eine neue, (…) motivierte Familie numerischer Integrationsverfahren vor. Im Gegensatz zu klassischen, polynombasierten Quadraturformeln approximiert der SK-Ansatz den Integranden durch (…): Die Arbeit entwickelt die mathematischen Grundlagen des Verfahrens, leitet seine Konvergenzordnung O(h4) her und zeigt, dass der SK-Integrator, ebenso wie die Simpson-Regel, Polynome bis zum Grad 3 exakt integriert, jedoch zusätzlich eine Klasse (…) Funktionen exakt erfasst. Kernbeitrag ist die kritische, reproduzierbare Evaluation des SK-Integrators im Vergleich zu etablierten Methoden. Die Ergebnisse bestätigen, dass der SK-Integrator nicht universell überlegen, sondern ein spezialisiertes Werkzeug ist: Sein Effizienzvorteil entfaltet sich primär bei Funktionen mit lokal (…)-ähnlicher Krümmung. Exemplarisch wird für f(x) = px auf [0; 1] eine Reduktion des relativen Fehlers um 56,2 % gegenüber der einfachen Simpson-Regel (bei gleichem Aufwand: 3 vs. 5 Funktionsauswertungen) nachgewiesen. Bei rein polynomialen oder stark asymmetrischen Integranden (z. B. x^3, 1/(1+ x2)) ist er hingegen weniger effizient. Die Arbeit leistet somit einen Beitrag zur differenzierten Methodenauswahl in der numerischen Integration: Sie zeigt, dass (…) Intuition zu innovativen algorithmischen Ansätzen führen kann, vorausgesetzt, deren Einsatzdomäne wird klar charakterisiert und ehrlich begrenzt. 

Dezember 2025